581A — Vasya the Hipster

The first number in answer (number of days which Vasya can dress fashionably) is min(a, b) because every from this day he will dress one red sock and one blue sock.

After this Vasya will have either only red socks or only blue socks or socks do not remain at all. Because of that the second number in answer is max((a - min(a, b)) / 2, (b - min(a, b)) / 2).

Asymptotic behavior of this solution — O(1).

581B — Luxurious Houses

This problem can be solved in the following way. Let's iterate on given array from the right to the left and will store in variable maxH the maximal height if house which we have already considered.Then the answer to house number i is number max(0, maxH + 1 - h_i), where h_i number of floors in house number i.

Asymptotic behavior of this solution — O(n), where n — number of houses.

581C — Developing Skills

This problem can be solved in many ways. Let's consider the most intuitive way that fits in the given time.

In the beginning we need to sort given array in the following way — from two numbers to the left should be the number to which must be added fewer units of improvements to make it a multiple of 10. For example, if given array is {45, 30, 87, 26} after the sort the array must be equal to {87, 26, 45, 30}.

Now we iterate on the sorted array for i from 1 to n. Let's cur = 10 - (a_imod10). If cur ≤ k assign a_i = a_i + cur and from k subtract cur else if cur > k break from cycle.

The next step is to iterate on array in the same way.

Now we need only to calculate answer ans — we iterate on array for i from 1 to n and assign ans = ans + (a_i / 10).

Asymptotic behavior of this solution — O(n * log(n)) where n is the number of hero skills.

581D — Three Logos

This problem can be solved in many ways, let's consider one of them.

The first step is to calculate sum of squares s of given rectangles. Then the side of a answer square is sqrt(s). If sqrt(s) is not integer print -1. Else we need to make the following.

We brute the order in which we will add given rectangles in the answer square (we can do it with help of next_permutation()) and for every order we brute will we rotate current rectangle on 90 degrees or not (we can do it with help of bit masks). In the beginning on every iteration the answer square c in which we add the rectangles is empty.

For every rectangle, which we add to the answer square we make the following — we need to find the uppermost and leftmost empty cell free in answer square c (recall that we also brute will we rotate the current rectangle on 90 degrees or not). Now we try to impose current rectangle in the answer square c and the top left corner must coinside with the cell free. If current rectangle fully placed in the answer square c and does not intersect with the some rectangle which has already been added, we need to fill by the required letter appropriate cells in the answer square c.

If no one of the conditions did not disrupted after we added all three rectangles and all answer square c is fully filled by letters we found answer and we neeed only to print the answer square c.

Else if we did not find answer after all iterations on the rectangles — print -1.

For random number of the rectangles k asymptotic behavior — O(k! * 2^k * s) where s — the sum of squares of the given rectangles.

Also this problem with 3 rectangles can be solved with the analysis of the cases with asymptotic O(s) where s — the sum of squares of given rectangles.

581E — Kojiro and Furrari

Let's f — the position of start, and e — the position of finish. For convenience of implementation we add the gas-station in point e with type equals to 3.

Note: there is never a sense go to the left of the starting point because we already stand with a full tank of the besr petrol. It is correct for every gas-station in which we can appear (if in optimal answer we must go to the left in some gas-station pv, why not throw out all the way from pv to current gas-station v and back and after that the answer will be better). Now let's say about algorithm when we are in some gas-station v.

The first case: on distance no more than s there is the gas-station with quality of gasoline not worse, than in the current gas-station. Now we fix nearest from them nv (nearest to the right because go to the left as we understand makes no sense). In that case we refuel in such a way to can reach nv and go to nv.

The second case: Второй случай: из нас достижимы только заправки с худшим качеством. Заметим, что это возможно лишь в случае, если мы находимся в заправке типа 2 или 3. В случае заправки второго типа у нас нет никакого выбора кроме как заправиться на полную и поехать в самую последнюю достижимую вершину (то есть вершину на расстоянии не более чем s). Если же мы находимся в вершине типа 3, то нужно идти по возможности в самую дальнюю вершину типа 2, если же такой нет то идти в самую дальнюю типа 1. Эти рассуждения верны в силу того, что нам в первую очередь необходимо минимзировать бензин типа 1, а при равенстве типа — 2. Как можно дальше нужно идти потому, что бензин в нашей вершине строго лучше достижимых, а тип 2 нужно выбирать, поскольку если мы можем доехать до типа 1 и он находится правее заправки типа 2, то мы можем это сделать, проехав через заправку типа 2, возможно улучшив ответ.

This basic reasoning necessary to solve the problem. The next step — calc dynamic on all suffixes i of gas-stations — the answer to the problem if we start from the gas-station i with empty tank. We need to make updates, considering the above cases. For update the dynamic in v we need to take the value of dynamic in nv and make update in addiction of the case. If the case is equals to 1, we need to add to appropriate value the distance d from v to nv. If this case is equals to 2 and we are in the gas-station with type equals to 2 we need to add s to the second value of answer, and from the first value we need to substract s–d. If it is the case number 2 and we are in the gas-station with type equals to 3, we need to substract from the value, which determined by the type of the gas-station nv, s–d.

Now to answer on specific query of the starting position we nned to find the first gas-station which is to the right of the startiong position, make one update and take the value of dynamic, which already calculated, and recalculate this value in accordance with the above.

Asymptotic behavior — O(n logn) or O(n) in case how we find position in the list of gas-stations (the first in case of binary search, the second in case of two pointers).

To this solution we need O(n) memory.

581F — Zublicanes and Mumocrates

Let the number of leavs in tree (vertices with degree 1) is equal to c. It said in statement that c is even. If in given graph only 2 vertices the answer is equal to 1. Else we have vertex in graph which do not a leaf — we hang the three on this vertex.

Now we need to count 2 dynamics. The first z1[v][cnt][col] — the least amount of colored edges in the subtree rooted at the vertex v, if vertex v already painted in color col (col equals to 0 or to 1), and among the top of the leaves of the subtree v must be exactly cnt vertices with color 0. If we are in the leaf, it is easy to count this value. If we are not in the leaf — we count value with help of dynamic z1[v][cnt][col]:  = z2[s][cnt][col], where s — the first child int the adjacency list of vertex v.

We need the second dynamic z2[s][cnt][col] to spread cnt leaves with color 0 among subtrees of childs of vertex v. To calc z2[s][cnt][col] we brute the color of child s — ncol and the number of childs i with color 0, which will be locate in subtree of vertex s and calc the value in the following way — z2[s][cnt][col] = min(z2[s][cnt][col], z2[ns][cnt–a][col] + z1[s][a][ncol] + (ncol! = col)), where ns — the next child of vertex v after the child s. Note, that it is senselessly to take a more than the number of leaves in the subtree s and to take more than the number of vertices in subtree — size_s (because in that case it will not be enough leaves for painting).

The upper bound of asymptotic for such dynamics O(n³). We show that in fact it works with asymptotic O(n²). Let's count the number of updates: 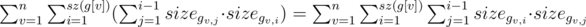. Note, that every pair of vertices (x, y) appears in the last sum (x, y) exactly once when v = lca(x, y). So we have no more than O(n²) updates.

Asymptotic behavior of this solution: O(n²).