581A — Хипстер Вася

Первое ответное число (количество дней, которое Вася сможет быть одет по моде) это min(a, b), так как каждый из этих дней он будет надевать по одному красному и по одному синему носку.

После этого у него останутся либо только красные носки, либо только синие носки, либо не останется носков вовсе. Поэтому второе ответное число это max((a - min(a, b)) / 2, (b - min(a, b)) / 2).

Асимптотика решения — O(1).

581B — Элитные дома

Данная задача решается следующим образом. Пойдем по массиву справа налево и будем поддерживать в переменной maxH максимальную высоту дома, который мы уже рассмотрели. Тогда ответом для i-го дома будет число max(0, maxH + 1 - h_i), где h_i количество этажей в i-м доме.

Асимптотика решения — O(n), где n — количество домов.

581C — Развитие навыков

Данную задачу можно решать несколькими способами. Рассмотрим самый понятный способ, который укладывается в заданное время.

Отсортируем заданный массив следующим образом — из двух чисел левее должно стоять то, к которому нужно добавить меньше единиц улучшений, чтобы оно стало кратно 10. Обязательно добавлять хотя бы одну единицу энергии. Например, если исходный массив {45, 30, 87, 26}, то после сортировки он должен выглядеть следующим образом — {87, 26, 45, 30}.

Теперь проитерируемся по отсортированному массиву слева направо по i от 1 до n. Пусть cur = 10 - (a_imod10). Если cur ≤ k, присвоим a_i = a_i + cur, а из k вычтем cur, иначе, если cur > k выйдем из цикла.

Следующим шагом проитерируемся по массиву аналогичным образом.

Осталось посчитать ответ ans — проитерируемся по массиву по i от 1 до n и присвоим ans = ans + (a_i / 10).

Асимптотика решения — O(n * log(n)), где n количество заданных навыков героя.

581D — Три логотипа

Данная задача решается несколькими способами, рассмотрим один из них.

Для начала подсчитаем суммарную площадь s данных нам прямоугольников. Тогда сторона ответного квадрата это sqrt(s). Если sqrt(s) не целое число, выводим -1. Иначе сделаем следующее.

Переберем порядок, в котором будем добавлять заданные прямоугольники в квадрат (это можно сделать с помощью next_permutation()), а также для каждого порядка переберем будем ли мы переворачивать текущий прямоугольник на 90 градусов или нет (это можно сделать с помощью двоичных масок). Изначально на каждой итерации квадрат c, в который мы добавляем прямоугольники ничем не заполнен (пустой).

Для каждого из добавляемых прямоугольников сделаем следующее — найдем самую верхнюю левую свободную клетку free в квадрате c (напомним, что мы также перебираем, поворачиваем ли мы прямоугольник на 90 градусов или нет). Попытаемся наложить текущий прямоугольник в квадрат c, причем его левый верхний угол должен совпадать с клеткой free. Если текущий прямоугольник полностью помещается в квадрат c и не накладывается на уже занятую каким-то другим прямоугольником клетку, заполним соответствующие клетки в квадрате c нужной буквой.

Если после добавления всех трех прямоугольников не нарушилось ни одно из условий и весь квадрат c оказался заполненным мы нашли ответ — выводим квадрат c.

Если ответ не нашелся ни для одной перестановки прямоугольников — выводим -1.

Для произвольного количества прямоугольников k асимптотика решения — O(k! * 2^k * s), где s — суммарная площадь заданных прямоугольников.

Также данная задача для 3 прямоугольников имеет решение с разбором случаев с асимптотикой O(s), где s — суммарная площадь заданных прямоугольников.

581E — Кодзиро и Furrari

Пусть f — стартовая позиция, а e — конечная. Для удобства реализации и дальнейших рассуждений добавим заправку в точке e типа 3.

Первое замечание: никогда нет смысла идти налево из стартовой точки ведь мы в ней уже стоит с полным баком лучшего бензина. Замечание верно и для любой заправки, в которой мы можем оказаться (если в оптимальном ответе мы должны пойти налево до некоторой заправки pv, то почему бы не выкинуть весь путь из pv в текущую заправку v и обратно и от этого ответ станет только лучше). Теперь поймем как нам следует действовать если мы находимся в некоторой заправке v.

Первый случай: на расстоянии не более чем s находится заправка в качеством бензина не хуже, чем в нашей (можно считать, что в момент старта мы находимся на заправке типа 3, но добавлять такую заправку нельзя). Зафиксируем ближайшую из них nv (ближайшую справа, так как мы уже поняли, что идти влево нет смысла). В этом случае дозаправимся так, чтобы возможно было доехать до nv. И поедем в nv.

Второй случай: из нас достижимы только заправки с худшим качеством. Заметим, что это возможно лишь в случае, если мы находимся в заправке типа 2 или 3. В случае заправки второго типа у нас нет никакого выбора кроме как заправиться на полную и поехать в самую последнюю достижимую вершину (то есть вершину на расстоянии не более чем s). Если же мы находимся в вершине типа 3, то нужно идти по возможности в самую дальнюю вершину типа 2, если же такой нет то идти в самую дальнюю типа 1. Эти рассуждения верны в силу того, что нам в первую очередь необходимо минимзировать бензин типа 1, а при равенстве типа — 2. Как можно дальше нужно идти потому, что бензин в нашей вершине строго лучше достижимых, а тип 2 нужно выбирать, поскольку если мы можем доехать до типа 1 и он находится правее заправки типа 2, то мы можем это сделать, проехав через заправку типа 2, возможно улучшив ответ.

Это основные рассуждения необходимые для решения задачи. Далее будем считать диманику на всех суффиксах i заправок — ответ на задачу если мы стартуем из заправки i с пустым баком. Переходы мы должны сделать, рассматривая описанные выше случаи. Для пересчета динамики в v нам нужно взять значение динамики в nv и сделать пересчет в зависимости от случая. Если случай 1, то нужно просто к соответствующему значению прибавить расстояние d от v к nv. Если это случай 2 и мы в заправке типа 2 нужно ко второму значению ответа прибавить s, а из первого вычесть s–d. Если это случай 2 и мы в заправке типа 3, то нужно из значения, определяемого типом заправки nv вычесть s–d.

Теперь, чтобы ответить на конкретный запрос стартовой позиции нужно найти первую завправку правее стартовой позиции, сделать один переход и взять уже посчитанное значение динамики (конечно, пересчитав это значение в соответствии с вышеописанным).

Сложность решения по времени: O(n logn) или O(n) в зависимости от того как искать позицию в списке заправок (первое в случае бинпоиска, второе в случае двух указателей). Сложность решения по памяти: O(n).

581F — Зубликанцы и мумократы

Пусть количество листьев дерева (вершин степени 1) равно c. По условию c четно. Если вершин всего 2, то ответ 1. Иначе в дереве есть вершина не лист, подвесим дерево за эту вершину.

Теперь будем считать 2 динамики. Первая z1[v][cnt][col] — наименьшее количество разноцветных ребер в поддереве с корнем в вершине v, если вершина v уже покрашена в цвет col (col равен 0 либо 1), а среди листьев поддерева вершины v должно быть ровно cnt вершин цвета 0. Если мы в листе, то это значение легко посчитать. Если мы не в листе посчитаем значение с помощью вспомогательной динамики z1[v][cnt][col]:  = z2[s][cnt][col], где s — первый сын в списке смежности вершины v.

Вторая динамика z2[s][cnt][col] нам нужна для того, чтобы распределить cnt листьев цвета 0 среди поддеревьев сыновей вершины v. Для подсчета z2[s][cnt][col] переберем цвет сына s — ncol и количество листьев i цвета 0, которые будут располагаться в поддереве вершины s и пересчитаем значение следующим образом z2[s][cnt][col] = min(z2[s][cnt][col], z2[ns][cnt–a][col] + z1[s][a][ncol] + (ncol! = col)), где ns — следующий после s сын вершины v. Заметим, что не имеет смысла брать a больше, чем количество листьев в поддереве s, ну и тем более — больше количества вершин в поддереве size_s (поскольку у нас просто не хватит листьев для покраски).

Оценка сверху для такой динамики O(n³). Покажем, что в сумме решение будет работать за O(n²). Посчитаем количество переходов: 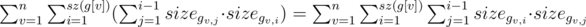. Заметим, что в последнюю сумму каждая пара вершин (x, y) войдет ровно один раз, именно при наименьшем общем предке v = lca(x, y). Таким образом переходов не более O(n²).

Сложность решения по времени и памяти: O(n²).