581A — Vasya the Hipster

The first number in answer (number of days which Vasya can dress fashionably) is min(a, b) because every from this day he will dress one red sock and one blue sock.

After this Vasya will have either only red socks or only blue socks or socks do not remain at all. Because of that the second number in answer is max((a - min(a, b)) / 2, (b - min(a, b)) / 2).

Asymptotic behavior of this solution — O(1).

581B — Luxurious Houses

This problem can be solved in the following way. Let's iterate on given array from the right to the left and will store in variable maxH the maximal height if house which we have already considered.Then the answer to house number i is number max(0, maxH + 1 - h_i), where h_i number of floors in house number i.

Asymptotic behavior of this solution — O(n), where n — number of houses.

581C — Developing Skills

This problem can be solved in many ways. Let's consider the most intuitive way that fits in the given time.

In the beginning we need to sort given array in the following way — from two numbers to the left should be the number to which must be added fewer units of improvements to make it a multiple of 10. For example, if given array is {45, 30, 87, 26} after the sort the array must be equal to {87, 26, 45, 30}.

Now we iterate on the sorted array for i from 1 to n. Let's cur = 10 - (a_imod10). If cur ≤ k assign a_i = a_i + cur and from k subtract cur else if cur > k break from cycle.

The next step is to iterate on array in the same way.

Now we need only to calculate answer ans — we iterate on array for i from 1 to n and assign ans = ans + (a_i / 10).

Asymptotic behavior of this solution — O(n * log(n)) where n is the number of hero skills.

581D — Three Logos

This problem can be solved in many ways, let's consider one of them.

The first step is to calculate sum of squares s of given rectangles. Then the side of a answer square is sqrt(s). If sqrt(s) is not integer print -1. Else we need to make the following.

We brute the order in which we will add given rectangles in the answer square (we can do it with help of next_permutation()) and for every order we brute will we rotate current rectangle on 90 degrees or not (we can do it with help of bit masks). In the beginning on every iteration the answer square c in which we add the rectangles is empty.

For every rectangle, which we add to the answer square we make the following — we need to find the uppermost and leftmost empty cell free in answer square c (recall that we also brute will we rotate the current rectangle on 90 degrees or not). Now we try to impose current rectangle in the answer square c and the top left corner must coinside with the cell free. If current rectangle fully placed in the answer square c and does not intersect with the some rectangle which has already been added, we need to fill by the required letter appropriate cells in the answer square c.

If no one of the conditions did not disrupted after we added all three rectangles and all answer square c is fully filled by letters we found answer and we neeed only to print the answer square c.

Else if we did not find answer after all iterations on the rectangles — print -1.

For random number of the rectangles k asymptotic behavior — O(k! * 2^k * s) where s — the sum of squares of the given rectangles.

Also this problem with 3 rectangles can be solved with the analysis of the cases with asymptotic O(s) where s — the sum of squares of given rectangles.

581E — Kojiro and Furrari

581F — Zublicanes and Mumocrates

Let the number of leafs in tree (vertices with degree 1) is equal to c. It said in statement that c is even. If in given graph only 2 vertices the answer is equal to 1. Else we have vertex in graph which do not a leaf — we hang the three on this vertex.

Now we nned to count 2 dynamics. The first z1[v][cnt][col] — the least amount of colored edges in the subtree rooted at the vertex v, if vertex v already has been уже покрашена в цвет col (col равен 0 либо 1), а среди листьев поддерева вершины v должно быть ровно cnt вершин цвета 0. Если мы в листе, то это значение легко посчитать. Если мы не в листе посчитаем значение с помощью вспомогательной динамики z1[v][cnt][col]:  = z2[s][cnt][col], где s — первый сын в списке смежности вершины v.

Вторая динамика z2[s][cnt][col] нам нужна для того, чтобы распределить cnt листьев цвета 0 среди поддеревьев сыновей вершины v. Для подсчета z2[s][cnt][col] переберем цвет сына s — ncol и количество листьев i цвета 0, которые будут располагаться в поддереве вершины s и пересчитаем значение следующим образом z2[s][cnt][col] = min(z2[s][cnt][col], z2[ns][cnt–a][col] + z1[s][a][ncol] + (ncol! = col)), где ns — следующий после s сын вершины v. Заметим, что не имеет смысла брать a больше, чем количество листьев в поддереве s, ну и тем более — больше количества вершин в поддереве size_s (поскольку у нас просто не хватит листьев для покраски).

Оценка сверху для такой динамики O(n³). Покажем, что в сумме решение будет работать за O(n²). Посчитаем количество переходов: 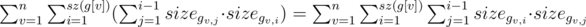. Заметим, что в последнюю сумму каждая пара вершин (x, y) войдет ровно один раз, именно при наименьшем общем предке v = lca(x, y). Таким образом переходов не более O(n²).

Сложность решения по времени и памяти: O(n²).