[problem:379553F]
There are not a lot of useful black squares.
Author: n0sk1ll
Consider this algorithm: iterate over all squares in the matrix and find the most distant black square.
Let's find out how to do that efficiently. In fact, only 4 (not necessarily distinct) squares will be useful: one square which minimizes $$$i-j$$$, one square which maximizes $$$i-j$$$, one square which minimizes $$$i+j$$$ and one square which maximizes $$$i+j$$$, where $$$(i,j)$$$ denotes the black cell's coordinates. In other words, we would like to find the most distant "border".
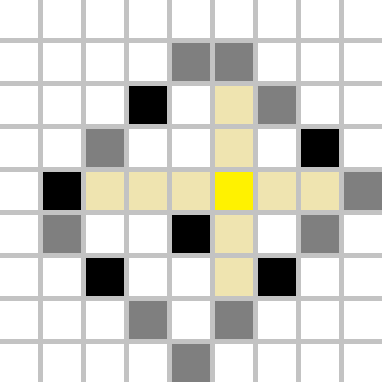
Let's look at the example above. The cell we choose to recolour to yellow creates four regions as shown. The most distant border will be fully contained inside one region, hence we should find distance from our yellow cell to any cell on that border, and that is the maximum possible distance.
#include <bits/stdc++.h>
using namespace std;
char tab[1003][1003];
pair<int,int> a={-1,-1},b={-1,-1},c={-1,-1},d={-1,-1};
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
int t; cin>>t;
while (t--)
{
a={-1,-1},b={-1,-1},c={-1,-1},d={-1,-1};
int n,m; cin>>n>>m;
for (int i=0;i<n;i++) cin>>tab[i];
vector<pair<int,int>> interesting;
for (int i=0;i<n;i++) for (int j=0;j<m;j++) if (tab[i][j]=='B')
{
if (a.first==-1 || i+j>a.first+a.second) a={i,j};
if (b.first==-1 || i+j<b.first+b.second) b={i,j};
if (c.first==-1 || i-j>c.first-c.second) c={i,j};
if (d.first==-1 || i-j<d.first-d.second) d={i,j};
}
interesting.push_back(a);
interesting.push_back(b);
interesting.push_back(c);
interesting.push_back(d);
int ans=1e9; pair<int,int> opt;
for (int i=0;i<n;i++) for (int j=0;j<m;j++)
{
int dist=0;
for (auto it : interesting) dist=max(dist,abs(i-it.first)+abs(j-it.second));
if (dist<ans) ans=dist,opt={i,j};
}
cout<<opt.first+1<<" "<<opt.second+1<<"\n";
}
}





