Hope you liked the problems!
This is my second contest on Codeforces, inspiring coordination has been done for the last several months, cannot wait until the third round is released!
| Tester | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| xiaoziya | 900 | 1000 | 1400 | 1800 | 2100 | 3000 |
| feecle6418 | 900 | 1200 | 1400 | 1700 | 2200 | 2900 |
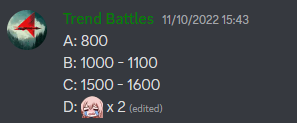
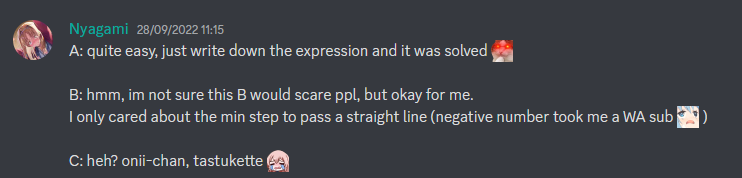
| ntherner | 800 | 1100 | 1550 | 1900 | 2200 | - |
| 6aren | 800 | 1200 | - | 2000 | 2200 | - |
| neko_nyaaaaaaaaaaaaaaaaa | 800 | - | - | 2100 | 2400 | 3000 |
| tibinyte2006 | 800 | 1100 | 1550 | 1800 | 2100 | 2550 |



Author: thanhchauns2
Try to brute force for $$$k < 50$$$. Do you see anything suspicious?
Now try to brute force from $$$k - 1$$$ to $$$0$$$ for large numbers.
1768A- Greatest Convex
Is $$$x = k - 1$$$ always suitable?
The answer is yes, as $$$x! + (x - 1)! = (x - 1)! \times (x + 1) = ((k - 1) - 1)! \times ((k - 1) + 1) = (k - 2)! \times (k)$$$, which is clearly a multiple of $$$k$$$.
Therefore, $$$x = k - 1$$$ is the answer.
Time complexity: $$$\mathcal{O}(1)$$$
answer = [print(int(input()) - 1) for testcase in range(int(input()))]
Author: Vladithur
Will be added later
Author: thanhchauns2
How many times a unique number can appear in the array $$$a$$$?
Can there be two numbers $$$1$$$ in $$$a$$$? What is the conclusion?
If you sort the array, which rules should the new array satisfy? Given the array $$$[1,2,2 ]$$$, is there any answer for this case?
Which element should you construct first?
1768C- Elemental Decompress
Two cases produce no answers:
One element appears more than twice in $$$a$$$.
After sorting, there is some index that $$$a[i] < i$$$ ($$$1$$$-indexed).
Consider there is some index that $$$a[i] <i$$$, then both $$$p[i] < i$$$ and $$$q[i] < i$$$ must satisfy. This is also true for the first $$$i - 1$$$ index, so the numbers that are smaller than $$$i$$$ in both $$$p$$$ and $$$q$$$ are $$$(i - 1) \times 2 + 2 = i * 2$$$. This is a contradiction.
Otherwise, solutions always exist. One method is to constructively attach each element in $$$a$$$ to $$$p$$$ or $$$q$$$:
Traverse from the biggest element to the smallest in $$$a$$$, if that number haven't appeared in $$$p$$$ then attach it to $$$p$$$, otherwise attach it to $$$q$$$.
Traverse from the biggest element to the smallest in $$$a$$$ again, if we attached it to $$$p$$$, find the biggest number that did not appear in $$$q$$$ and attach to $$$q$$$, vice versa.
A naive solution requires the $$$O(n^2)$$$ method to solve. We can reduce to $$$O(N log N)$$$ by sorting element in $$$a$$$ as pairs <element, index>.
Time complexity: $$$\mathcal{O}(n \log(n))$$$
#include <bits/stdc++.h>
using namespace std;
const int N = 200005;
int n;
int a[N], b[N], c[N], ra[N], rb[N];
void out()
{
for (int i = 0; i < n; i++)
{
cout << a[i] << ' ';
}
cout << '\n';
for (int i = 0; i < n; i++)
{
cout << b[i] << ' ';
}
cout << '\n';
}
void solve()
{
cin >> n;
vector<pair<int, int> > V;
for (int i = 0; i < n; i++)
{
cin >> c[i];
a[i] = b[i] = 0;
ra[i + 1] = rb[i + 1] = 1;
V.push_back(make_pair(c[i], i));
}
sort(V.rbegin(), V.rend());
for (int i = 0; i < n; i++)
{
int k = V[i].second;
if (ra[c[k]] == 1) a[k] = c[k], ra[c[k]]--;
else b[k] = c[k], rb[c[k]]--;
}
int r1 = n, r2 = n;
for (int i = 0; i < n; i++)
{
int k = V[i].second;
if (a[k] == 0)
{
while (ra[r1] == 0) r1--;
ra[r1]--;
if (r1 > b[k])
{
cout << "NO" << '\n';
return;
}
a[k] = r1--;
}
else
{
while (rb[r2] == 0) r2--;
rb[r2]--;
if (r2 > a[k])
{
cout << "NO" << '\n';
return;
}
b[k] = r2--;
}
}
for (int i = 1; i <= n; i++)
{
if (ra[i] != 0 || rb[i] != 0)
{
cout << "NO" << '\n';
return;
}
}
cout << "YES" << '\n';
out();
}
int main(int argc, char* argv[])
{
ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0);
int t;
cin >> t;
while(t--)
solve();
}
Author: Vladithur
Will be added later
Author: thanhchauns2
Given a fixed permutation, how many operations do we need to sort it?
Keep in mind there is one already sorted permutation that doesn't need to be sorted.
What if there is exactly $$$1$$$ number in the range $$$[n + 1, 2n]$$$ that appears in the first $$$n$$$ numbers?
This is not really a hint, fft solutions exist, but we made sure most of them cannot pass.
1768E- Partial Sorting
We need at most $$$3$$$ operations to sort the permutation: $$$1 -> 2 -> 1$$$
- For $$$f(p) = 0$$$, there is only one case: the initially sorted permutation.
return (38912738912739811 & 1)
- For $$$f(p) \leq 1$$$, this scenario appears when the first $$$n$$$ numbers or the last $$$n$$$ numbers are in the right places.
Both cases have $$$n$$$ fixed positions, so there will be $$$(2n!)$$$ permutations in each case.
Intersection: since both cases share the $$$n$$$ middle elements, $$$(n!)$$$ permutation will appear in both cases.
So there will be $$$2 \times (2n!) - (n!)$$$ such permutations.
- For $$$f(p) \leq 2$$$, this scenario appears when the smallest $$$n$$$ elements' positions are in range $$$[1, 2n]$$$, or the largest $$$n$$$ numbers' positions are in range $$$[n + 1, 3n]$$$.
If the smallest $$$n$$$ elements are all in position from $$$1$$$ to $$$2n$$$, then:
There are $$$C_{2n}^{n}$$$ ways to choose $$$n$$$ positions for these numbers.
For each way to choose these positions, there are $$$n!$$$ ways to choose the position for the smallest $$$n$$$ numbers, and $$$2n!$$$ ways for the rest.
The total number of valid permuations are: $$$C_{2n}^{n} \times n! \times 2n!$$$
If the largest $$$n$$$ elements are all in position from $$$n + 1$$$ to $$$3n$$$, we do the same calculation.
Intersection: intersection appears when the first $$$n$$$ numbers are all in range $$$[1, 2n]$$$ and the last $$$n$$$ numbers are all in range $$$[n + 1, 3n]$$$.
Let intersection = 0
Let's talk about the numbers in range $$$[n + 1, 2n]$$$. There are $$$n$$$ such numbers.
. Imagine there are EXACTLY $$$0$$$ numbers in this range that appear in the first $$$n$$$ numbers. So:
In the first $$$n$$$ numbers there are $$$n$$$ numbers in range $$$[1, n]$$$. There are $$$C_{n}^{n} \times n!$$$ cases.
In the first $$$n$$$ numbers there are $$$0$$$ numbers in range $$$[n + 1, 2n]$$$. There are $$$C_{n}^{0} \times n!$$$ cases.
In the last $$$n$$$ numbers there are $$$n$$$ numbers in range $$$[n + 1, 2n]$$$, we have used $$$0$$$ numbers for the first n numbers. There are $$$C_{2n}^{n} \times n!$$$ cases.
Then we have: intersection += $$$C_{n}^{n} \times C_{n}^{0} \times C_{2n}^{n} \times n! \times n! \times n!$$$
How about there is EXACTLY $$$1$$$ number in range [n + 1, 2n] appearing in the first n numbers?
In the first $$$n$$$ numbers there are $$$n - 1$$$ numbers in range $$$[1, n]$$$. There are $$$C_{n}^{n - 1} \times n!$$$ cases.
In the first $$$n$$$ numbers there are $$$1$$$ numbers in range $$$[n + 1, 2 * n]$$$. There are $$$C_{n}^{1} \times n!$$$ cases.
In the last $$$n$$$ numbers there are $$$n$$$ numbers in range $$$[n + 1, 2 * n]$$$, we have used $$$1$$$ numbers for the first $$$n$$$ numbers. There are $$$C_{2n - 1}^{n} \times n!$$$ cases.
Then we have: intersection += $$$C_{n}^{n - 1} \times C_{n}^{1} \times C_{2n - 1}^{n} \times n! \times n! \times n!$$$
... And so on
The number of intersections will be equal to: $$$ \sum_{i = 1}^{n} C_{n}^{n - i} \times C_{n}^{i} \times C_{2n - i}^{n} \times n! \times n! \times n! $$$
- For $$$f(p) \leq 3$$$, it will be the count of all valid permutations.
return __fraction(3 * __number_of_sides_of_a_triangle + __thanhchauns2_will_reach_GM)
Time complexity: $$$\mathcal{O}(n)$$$
#include <bits/stdc++.h>
using namespace std;
long long n, M;
long long frac[3000005], inv[3000005];
long long powermod(long long a, long long b, long long m)
{
if (b == 0) return 1;
unsigned long long k = powermod(a, b / 2, m);
k = k * k;
k %= m;
if (b & 1) k = (k * a) % m;
return k;
}
void Ready()
{
frac[0] = 1;
inv[0] = 1;
for (int i = 1; i <= 3000000; i++)
{
frac[i] = (frac[i - 1] * i) % M;
}
inv[3000000] = powermod(frac[3000000], M - 2, M);
for (int i = 3000000; i > 0; i--)
{
inv[i - 1] = (inv[i] * i) % M;
}
}
long long C(long long n, long long k)
{
return ((frac[n] * inv[k]) % M * inv[n - k]) % M;
}
int main()
{
cin >> n >> M;
Ready();
long long ans[4]{};
// X = 0
ans[0] = 1;
// X = 1
ans[1] = 2 * frac[2 * n] - frac[n] - ans[0] + M + M;
ans[1] %= M;
// X = 2
ans[2] = frac[2 * n];
ans[2] = ans[2] * C(2 *n, n) % M;
ans[2] = ans[2] * frac[n] % M;
ans[2] = ans[2] * 2 % M;
for (int i = 0; i <= n; i++)
{
int sub = C(n, i);
sub = sub * C(n, n - i) % M;
sub = sub * C(2 * n - i, n) % M;
sub = sub * frac[n] % M;
sub = sub * frac[n] % M;
sub = sub * frac[n] % M;
ans[2] = (ans[2] - sub + M) % M;
}
ans[2] = (ans[2] - ans[1] + M) % M;
ans[2] = (ans[2] - ans[0] + M) % M;
// X = 3
ans[3] = frac[3 * n];
ans[3] = (ans[3] - ans[2] + M) % M;
ans[3] = (ans[3] - ans[1] + M) % M;
ans[3] = (ans[3] - ans[0] + M) % M;
long long answer = ans[1] + 2 * ans[2] + 3 * ans[3];
answer %= M;
cout << answer << endl;
}
Author: Vladithur
Use dynamic programming.
$$$a_i \le n$$$
Compare $$$\min(a_i \ldots a_j) \cdot (j - i)^2$$$ with $$$n \cdot (j - i)$$$.
Compare $$$\min(a_i \ldots a_j) \cdot (j - i)^2$$$ with $$$\min(a_i \ldots a_k) \cdot (k - i)^2 + \min(a_k \ldots a_j) \cdot (j - k)^2$$$ for some $$$i < k < j$$$.
Two cases: $$$\min(a_i \ldots a_j) \ge \sqrt{n}$$$ and $$$\min(a_i \ldots a_j) < \sqrt{n}$$$.
Split $$$\min(a_i \ldots a_j) < \sqrt{n}$$$ into two more cases: $$$\min(a_i \ldots a_j) = a_i$$$ and $$$\min(a_i \ldots a_j) = a_j$$$.
~~~~~
~~~~~





