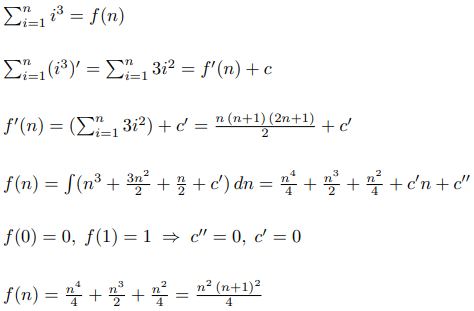Допустим, вы хотите для некоторых n и k найти сумму:
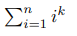
Вот известные формулы для первых нескольких k:
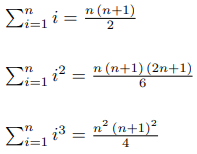
Допустим, вы забыли их. Что делать? К счастью, существует простой алгоритм для генерации этих формул.
Прежде всего докажем теорему.
Теорема
Предположим, что для каждого целого неотрицательного n:
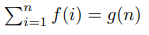
где f и g – многочлены. Тогда для некоторой константы c:
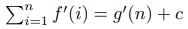
Доказательство
Для каждого целого положительного n верно:
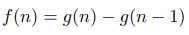
Эти два многочлена равны в бесконечном количестве точек, а значит, они тождествены. Что позволяет нам сказать:
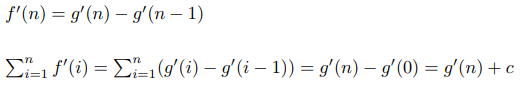
Применение
Допустим, мы хотим найти формулу для суммы квадратов. Тогда, используя нашу теорему, можно построить такой алгоритм:
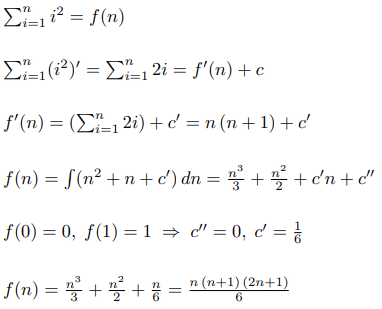
Теперь проделаем тот же алгоритм для суммы кубов: