Nowcoder problem (Chinese) link. The submission is private because I don't want to publish my Nowcoder account, but you can copy the code at the end of this blog and paste it to the answer sheet, it will get AC.
First I would like to thank ShaoNianTongXue5307 for his idea!
This is a learning note, most for myself. Most of this blog is not original.
Part 1: Problem Statement:
A tree $$$T=(V, E)$$$ has $$$n$$$ vertices and $$$n-1$$$ edges, the weight of each vertex $$$i$$$ is $$$a_i$$$.
For each edge $$$e$$$, you can determine its direction, i.e., for two vertices $$$u, v$$$, there are two states: $$$u \rightarrow v$$$ and $$$v \rightarrow u$$$. There are $$$2^{n-1}$$$ states in total.
For each state $$$S$$$, we define $$$f(S)$$$ as
$$$f(S) := \sum\limits_{(u, v) \in V \times V, v\,\text{is reachable from}\,u} |a_u - a_v|$$$.
Compute the sum of $$$f(S)$$$ over all $$$2^{n-1}$$$ states $$$S$$$, modulo $$$998244353$$$.
Example:
Suppose $$$n=3$$$, and two edges connect $$$(1, 2), (2, 3)$$$, respectively. $$$a_1 = 3, a_2 = 1, a_3 = 2$$$, the answer is $$$14$$$.
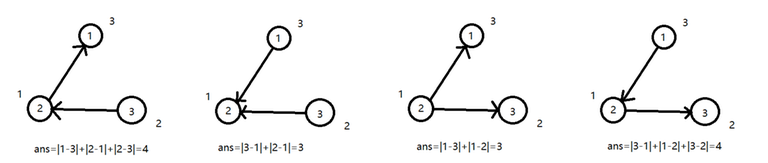
Constraints: $$$2 \leq n \leq 2 \cdot 10^5$$$, $$$1 \leq a_i \leq 10^9$$$.
Part 2: What is the centroid decomposition good at?
Before we learn centroid decomposition, we should first know what it is good at. For a tree $$$T = (V, E)$$$, we can decompose $$$V$$$ into $$$V = V_1 \cup V_2 \cup ... \cup V_t$$$, where $$$V_i (1 \leq i \leq t)$$$ are pairwise disjoint non-empty sets. $$$V_1$$$ is a singleton which contains only one element: The centroid. $$$V_2, ..., V_t$$$ are the connected components of $$$T \setminus V_1$$$. We want to calculate some function $$$f(T)$$$, and we assume that the base case, where $$$V(T) = 1$$$, is easy to calculate. This assumption is not strict, because if we can't even deal with the case where $$$V(T)=1$$$, we can actually achieve nothing. The another important function besides $$$f$$$ is the merge function: $$$merge(V_1, V_2, ..., V_t)$$$. Formally
$$$f(V) = \sum\limits_{i=1}^t f(V_i) + merge(V_1, V_2, ..., V_t)$$$. (1)
Like the merge sort, the number of iterations in the centroid decomposition algorithm is $$$O(log |V|)$$$, so it takes roughly $$$O(log |V| \cdot merge)$$$ times. Therefore, the most important advantage to use centroid decomposition is that the merge function could be computed fast enough. Otherwise, it is even slower than the brute force! In our solution merge is $$$O(|V|log|V|)$$$ so its complexity is $$$O(|V|log^2|V|)$$$. You may recall the process of the merge sort if you have trouble understanding these words.
Part 3: What is a centroid, and what is a centroid decomposition?
For a tree, the vertex $$$v$$$ is called a centroid if and only if for any subtree rooted at v’s child has a size at most half the size of the original tree rooted at $$$v$$$. For example, the centroids for the path A--B--C--D are B and C.
Property $$$1$$$: A tree has one or two centroids.
Proof: First, we prove that one tree has at least one centroid. The centroid could be found using a constructive algorithm. First we specify an original root $$$r$$$. Initialize $$$v$$$ as $$$r$$$. Check whether $$$v$$$ is a centroid. If yes, we have already done. If not, replace $$$v$$$ with $$$v$$$'s heavy child $$$u$$$, i.e., $$$argmax(u)\{size[u] \mid u\,\text{is}\,v\text{'s child}\}$$$. The iteration will terminate since the size if finite. When it terminates, the size of subtrees rooted at $$$v$$$'s children $$$\leq \frac{|V|}{2}$$$. We need to be careful that, when the tree is rooted at $$$v$$$ (instead of $$$r$$$), the parent of $$$v$$$ in the $$$r$$$-rooted tree becomes a child of $$$v$$$ in the $$$v$$$-rooted tree, so we need to check the parent of $$$v$$$ in the $$$r$$$-rooted tree. Since the algorithm does not terminate at $$$v$$$'s parent, the size of $$$v \leq \frac{|V|}{2}$$$, therefore, (the size of $$$v$$$'s parent) — (the size of $$$v$$$'s parent) $$$\leq \frac{|V|}{2}$$$, which also satisfies the condition.
Second, we prove that one tree has at most two centroids. Suppose $$$a$$$ and $$$b$$$ are two centroids. Then, there is a subtree of $$$a$$$'s child ($$$A$$$) containing $$$b$$$, and a subtree of $$$b$$$'s child ($$$B$$$) containing $$$a$$$, $$$A \cup B = V, |A|, |B| \leq \frac{|V|}{2}$$$. By the principle of inclusion-exclusion (PIE), $$$A$$$ and $$$B$$$ must be disjoint, therefore there is an edge $$$ab$$$. So there cannot be $$$\geq 3$$$ centroids, and if it contains $$$2$$$ centroids, these two centroids must be adjacent.
Property $$$2$$$: $$$v := argmin(v)\{max\{size[u] \mid u\,\text{is}\,v\text{'s child in the tree rooted at }v\}\}$$$ is a centroid. This can be proved using the fact that every tree has at least one centroid, so the "best" vertex must be a centroid. In English, for a vertex $$$v$$$, lets the score of $$$v$$$ be the maximum size of subtrees rooted at $$$v$$$'s children in the $$$v$$$-rooted tree. The $$$v$$$ with the minimum score is the centroid.
For example, the edges are $$$(A, B), (B, D), (B, C), (C, E)$$$. The scores of $$$A,B,C,D,E$$$ are $$$4, 2, 3, 4, 4$$$ respectively, so the centroid is $$$B$$$.
Property $$$3$$$: $$$v$$$ is a centroid if and only if for arbitrary $$$q \in V$$$, $$$\sum\limits_{u \in V} d(u, v) \leq \sum\limits_{u \in V} d(u, q)$$$.
Proof: $$$\rightarrow$$$: $$$v$$$ is a centroid. Let's $$$qs$$$ be the size of subtree of $$$v$$$'s child that contains $$$q$$$. For the $$$qs2$$$ part, each vertex decreases $$$d(q, v)$$$, for the $$$|V|-qs$$$ part, each vertex increases $$$d(q, v)$$$, and for the $$$qs-qs2$$$ part, we don't know exactly, but each of vertex decreases at most $$$d(q, v)$$$ (if $$$qs > qs2$$$, the upper bound of total decrease $$$(qs-qs2)d(q, v)$$$ cannot be achieved), so the general distance sum increases when $$$v$$$ moves to $$$q$$$ as $$$qs \leq \frac{|V|}{2}$$$ by the definition of the centroid.
$$$\leftarrow$$$: If $$$qs > qs2$$$, then the $$$qs-qs2$$$ part decreases strictly less then $$$(qs-qs2) \cdot d(q, v)$$$, and the $$$qs$$$ part decreases strictly less then $$$qs \cdot d(q, v) \leq (|V| - qs) \cdot d(q, v)$$$. Therefore, $$$qs = qs2 = \frac{|V|}{2}$$$. There fore $$$q$$$ and $$$v$$$ are adjacent, the size of subtree rooted at $$$v$$$ in a $$$q$$$-rooted tree is $$$\frac{|V|}{2}$$$, therefore $$$q$$$ is a centroid.
Property $$$4$$$: Suppose $$$v$$$ is a centroid of the original tree $$$T$$$. If one leaf node is added to or deleted from $$$T$$$, then there is a centroid of $$$T$$$ (after operation) among $$$\{v\} \cup N(v)$$$, where $$$N(v)$$$ is the neighbor of $$$v$$$. Simply speaking, if $$$v$$$ is not a centroid after adding that leaf, we can replace $$$v$$$ with one of $$$v$$$'s child whose subtree contains that leaf. If $$$v$$$ is not a centroid after deleting that leaf, we can replace $$$v$$$ with $$$v$$$'s heavy child.
Centroid decomposition is a recursion process. Just find one centroid of the tree (if there are two centroid, find an arbitrary one of it), delete the centroid and the edges connecting to it. After that, the tree is decomposed into several connected components. Then, we do such decomposition for every connected component. Stop the recursion process if the vertex set of the tree is a singleton. Since each iteration halves the size, the centroid decomposition takes at most $$$O(log|V|)$$$ rounds.
Code: My code is adapted from this blog by lingfunny. It can AC ABC291EX Balanced Tree, submission is here. I paste the core code here:
struct cdt{
//cdt: Centroid Decomposition Tree
const int cdtINF = 0x7fffffff;
int *mxsz, *sz, *p, rt, nm;
//sz(x): The size of x
//mxsz(x): max{sz(y)|y is a child of x}
//p parent
bool* vis; //for convenience, we don't use a bitset here. But we can!
std::vector<int>* g;
cdt(int n):rt(0), nm(n){
assert(n > 0);
mxsz = new int[n+1];
mxsz[0] = cdtINF;
sz = new int[n+1];
p = new int[n+1];
g = new std::vector<int>[n+1];
vis = new bool[n+1];
memset(vis, 0, (n+1)*sizeof(bool));
}
~cdt(){
delete[] mxsz;
delete[] sz;
delete[] g;
delete[] vis;
}
void addedge(int u, int v){
g[u].push_back(v);
g[v].push_back(u);
}
void calcsize(int u, int fa){
mxsz[u] = sz[u] = 1;
for(int v: g[u]){
if(!vis[v] && v != fa){
calcsize(v, u);
sz[u] += sz[v];
mxsz[u] = std::max(mxsz[u], sz[v]);
}
}
mxsz[u] = std::max(mxsz[u], nm-sz[u]);
//mxsz最小的一定是树的重心, 因为一棵树至少有一个重心, 可能有1个或2个重心
//The argmin mxsz has to be the centroid, because one tree has at least one centroid!
if(mxsz[u] <= mxsz[rt]) rt = u;
}
void operate(int u, int fa){
calcsize(u, -1), calcsize(rt, -1), p[rt] = fa, dfz(rt);
}
void dfz(int u){
vis[u] = 1;
for(int v: g[u]){
if(!vis[v]){
nm = sz[v], rt = 0;
operate(v, u);
}
}
//Merge should be here.
}
};
int main(void){
int n;
cin >> n;
cdt c(n);
for(int i = 1, u, v; i <= n; ++i){
cin >> u >> v;
c.addedge(u, v);
}
c.operate(1, -1);
}
This code is a little bit comprehensive. It contains three recursions: operate, calcsize and dfz. It starts with operate, operate will call calcsize and dfz. calcsize will call itself and dfz will call operate in turn. The calcsize function is easier to understand, it has two usage: Calculate the size of each subtree, and find the centroid. Note that we call calcsize twice in the operation function, that is quite necessary: In the first call, we find the centroid, and in the second call, we find the size of each connected components. Then, the operation function calls the dfz function. In the initial call of dfz, i.e., the call from operation rather than the call from dfz itself, the parameter int u is guaranteed to be a centroid, so it recursively removes this centroid $$$V_1$$$ and decomposes $$$T \setminus V_1$$$ into connected components $$$V_2, V_3, ..., V_t$$$. The father (parent) of the centroids of $$$V_2$$$, $$$V_3$$$, ..., $$$V_t$$$ are all $$$V_1$$$, this is achieved using p[rt] = fa. There is no merge (described in the Part 2) operations in the code above. If there is a merge operation, we should place it at the end of the dfz function.
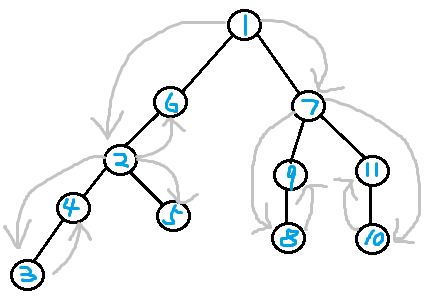
This is a graph from Xing-Ling's blog. $$$1$$$ is the centroid of the original tree. If we cut $$$1$$$, we get two connected components: $$$\{2,3,4,5,6\}$$$ and $$$\{7,8,9,10,11\}$$$. The centroids of these two connected components are $$$2$$$ and $$$7$$$ respectively, so the fathers (parents) of $$$2$$$ and $$$7$$$ are both $$$1$$$. Then we do the centroid decomposition in each component...
Part 4: Back to the original problem: How should we write the merge function?
This part is similar to the EATROCK from CodeChef Starter80A. The original Nowcoder problem is much harder than this CodeChef problem, only $$$8$$$ participants solve it.
In the merge function, we only consider $$$u$$$ and $$$v$$$ are from the different components in each iteration. In this case, $$$d(u, v) = dep(u) + dep(v)$$$, where $$$dep(\cdot)$$$ denotes the depth of $$$\cdot$$$ in the current tree. For $$$u$$$ and $$$v$$$ from different components, if $$$v$$$ is reachable from $$$u$$$, then $$$d(u, v) = dep(u) + dep(v)$$$ edges have to be fixed, so there are $$$n - dep(u) - dep(v) - 1$$$ free edges. So each $$$(u, v)$$$ pair appears $$$2^{n - dep(u) - dep(v) - 1}$$$ times, contributing $$$2^{n - dep(u) - dep(v) - 1}|a_u - a_v|$$$ to the final answer. The total contribution in each decomposition iteration is
$$$2^n \sum\limits_{a_v \leq a_u} (a_u - a_v)2^{-dep(u)-dep(v)} = 2^n \sum\limits_{u} a_u2^{-dep(u)}(\sum\limits_{v, a_v \leq a_u}2^{-dep(v)}) - \sum\limits_{u}2^{-dep(u)}(\sum\limits_{v, a_v \leq a_u}a_v2^{-dep(v)})$$$ (2).
Then, we can implement the merge by sorting $$$a$$$ and maintaining two prefix sums: $$$\sum\limits_{v} a_v2^{-dep(v)}$$$ and $$$\sum\limits_{v} 2^{-dep(v)}$$$. The complexity is $$$O(|V|log|V|)$$$ for each iteration because the sorting is a bottleneck. The overall complxity is $$$O(|V|log^2|V|)$$$ with a slightly larger constant, but the nowcoder machine is really fxxking fast. Code (645ms):






