Nowcoder problem (Chinese) link
First I would like to thank ShaoNianTongXue5307 for his idea!
This is a learning note, most for myself. Most of this blog is not original.
Part 1: Problem Statement
A tree $$$T=(V, E)$$$ has $$$n$$$ vertices and $$$n-1$$$ edges, the weight of each vertex $$$i$$$ is $$$a_i$$$.
For each edge $$$e$$$, you can determine its direction, i.e., for two vertices $$$u, v$$$, there are two states: $$$u \rightarrow v$$$ and $$$v \rightarrow u$$$. There are $$$2^{n-1}$$$ states in total.
For each state $$$S$$$, we define $$$f(S)$$$ as
$$$f(S) := \sum\limits_{(u, v) \in V \times V, v\,\text{is reachable from}\,u} |a_u - a_v|$$$.
Compute the sum of $$$f(S)$$$ over all $$$2^{n-1}$$$ states $$$S$$$, modulo $$$998244353$$$.
Example:
Suppose $$$n=3$$$, and two edges connect $$$(1, 2), (2, 3)$$$, respectively. $$$a_1 = 3, a_2 = 1, a_3 = 2$$$, the answer is $$$14$$$.
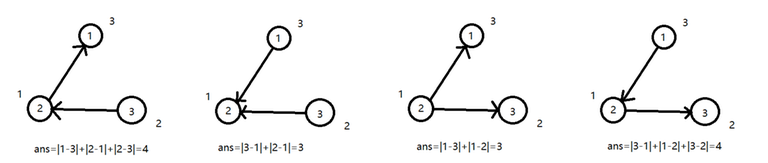
Constraints: $$$2 \leq n \leq 2 \cdot 10^5$$$, $$$1 \leq a_i \leq 10^9$$$.
Part 2: What is the centroid decomposition good at?:
Before we learn centroid decomposition, we should first know what it is good at. For a tree $$$T = (V, E)$$$, we can decompose $$$V$$$ into $$$V = V_1 \cup V_2 \cup ... \cup V_n$$$, where $$$V_i (1 \leq i \leq n)$$$ are pairwise disjoint non-empty sets. $$$V_1$$$ is a singleton which contains only one element: The centroid. We want to calculate some function $$$f(T)$$$, and we assume that the base case, where $$$V(T) = 1$$$, is easy to calculate. This assumption is not strict, because if we can't even deal with the case where $$$V(T)=1$$$, we can actually achieve nothing. The another important function besides $$$f$$$ is the merge function: $$$merge(V_1, V_2, ..., V_n)$$$. Formally
$$$f(V) = \sum\limits_{i=1}^n f(V_i) + merge(V_1, V_2, ..., V_n)$$$.
Like the merge sort, in the centroid decomposition algorithm






