Stirling Transformations

#	User	Rating
1	tourist	4009
2	jiangly	3831
3	Radewoosh	3646
4	jqdai0815	3620
4	Benq	3620
6	orzdevinwang	3529
7	ecnerwala	3446
8	Um_nik	3396
9	gamegame	3386
10	ksun48	3373

#	User	Contrib.
1	cry	164
1	maomao90	164
3	Um_nik	163
4	atcoder_official	160
5	-is-this-fft-	158
6	awoo	157
7	adamant	156
8	TheScrasse	154
8	nor	154
10	Dominater069	153

Hello, Codeforces!

1. Recently, adamant published an excellent blog Stirling numbers with fixed n and k. There he described an approach to them via generating functions.

In this (messy) blog, I want to share one useful technique on the example of Stirling numbers of the first kind.

2. We start with the definition of the Stirling transformation of a sequence $$$(x_n)$$$ is the following mapping

$$$\displaystyle \{x_n\} \xrightarrow{\quad Stirling\quad} \left\{ \sum_{k=0}^{n} s(n,k) x_k \right\}, $$$

where $$$s(n,k)$$$ is a first-kind Stirling number. Here we have a place of flexibility for our technique: we can choose any other function $$$f(n,k)$$$ instead of Stirling numbers, though it only sometimes turns out to be useful.

3. The essence of this method is to find the transition formulae between Stirling transformations of a sequence $$$(x_n)$$$ and the sequence of its finite differences (one can think of it as a discrete analogue of derivative) $$$(y_n)$$$ defined by

$$$\displaystyle \{x_n\} \xrightarrow{\quad \Delta\quad} \{x_{n+1}-x_n\}. $$$

The acquaintance with finite differences is highly recommended for the readers of this blog.

Theorem 1 (Transition formulae). In fact, the following transition formulae hold:

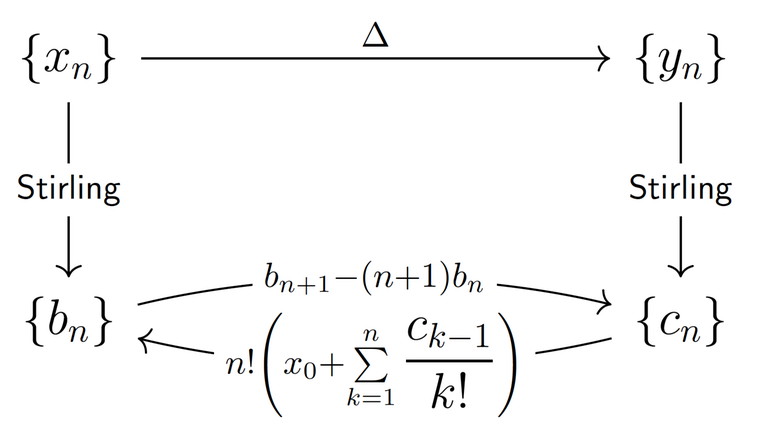
Step 1. How to work with finite differences?

Theorem 2 (solving first-order linear difference equation). Let $$$(y_k)$$$ be a recurrence relation that satisfies

$$$\displaystyle y_{k+1} = p_k y_{k} + q_k, $$$

where $$$(p_k), (q_k)$$$ are given sequences and there is no $$$i$$$ such that $$$p_i=0$$$, then the solution to this equation is given by

$$$\displaystyle y_k = \prod_{j=0}^{k-1} p_j \left( \sum_{j=0}^{k-1} \frac{q_j}{\prod_{\ell=0}^{j} p_\ell } + C\right) $$$

Proof

Step 2. Proof of the Theorem 1.

Proof

4. Using these transition formulae we can derive countless identities with Stirling numbers of the first kind (as well as identities involving binomial coefficients and other interesting combinatorial functions, as pointed out in 2). For example, taking $$$x_n = 1$$$, we obtain the following nice identity

$$$\displaystyle \sum_{k=0}^{n} s(n,k) = n! $$$

visualised by the diagram

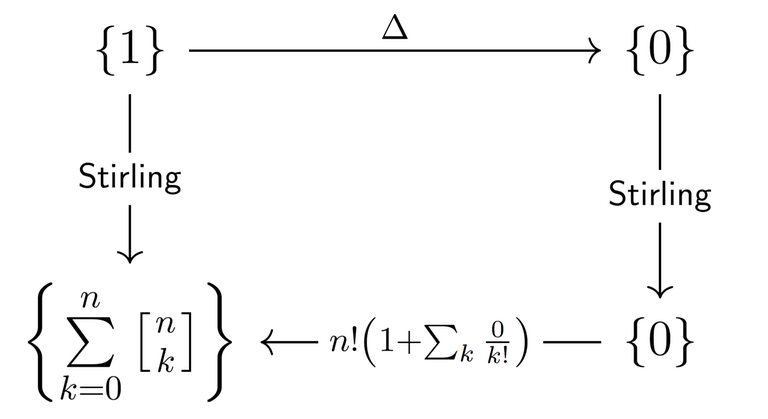
5. A nontrivial and interesting example. We exploit the combinatorial nature of $$$s(n,k)$$$ to write down the average number of cycles in a random permutation.

$$$\displaystyle \mathbf{E}[cycles] = \sum_{k=0}^{n} k \frac{s(n,k)}{n!} = \frac{\sum\limits_{k=0}^{n} k s(n,k)}{n!}. $$$

We can easily find the sum in the numerator by applying theorem 1 to the sequence $$$x_n = n$$$.

where the ($$$\ast$$$) is given by the following formula $$$\displaystyle \sum\limits_{k=0}^{n} k s(n,k) = n!\sum_{k=1}^{n} \frac{(k-1)!}{k!} = n!H_n, $$$

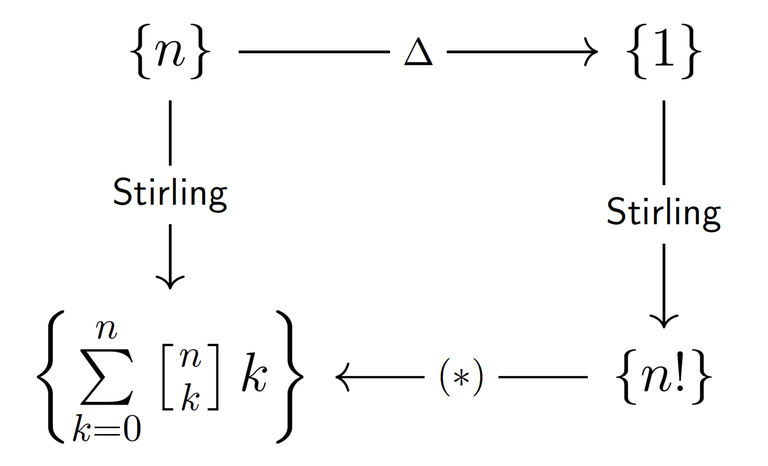
where $$$H_n = 1 + 1/2 + \dots + 1/n$$$ is $$$n$$$-th Harmonic number. Hence $$$\mathbf{E}[cycles]=H_n=O(\log n)$$$, a very nice result!

Exercise

6. We generalise 5 and 6 by consider the sequence $$$x_n = n^k$$$ for a fixed $$$k$$$. From adamant's blog (highly connected with this section), we know that first-kind Stirling numbers behave much better with falling factorials. So, in order to find a good formula for the Stirling transformation of $$$n^k$$$, we first find it for $$$(n)_k$$$ and then apply

$$$\displaystyle n^k = \sum_{j=0}^{k} S(n,j) (n)_j. $$$

and derive the desired formula.

The details are left for the reader, here is the outline.

Step 1. Prove the identity $$$\sum_{j=0}^{N} s(j,k)/j! = 1/N! s(N+1,k+1)$$$ by double induction and Pascal-like identity (lemma 1).

Step 2. Apply Theorem 1 to $$$x_n=(n)_k$$$ (fix $$$k$$$) and using 1 prove that

$$$\displaystyle \sum_{n=0}^{N} s(N,n) (n)_k = k! s(N+1, k+1). $$$

Step 3. Finally, prove that

$$$\displaystyle \sum_{j=0}^{N} s(N,n) n^k = \sum_{j=1}^{k} S(k,j) s(N+1, j+1) j!. $$$

The last formula is obviously practical.

7 (Bonus).

Theorem 3 (transition between two kinds of Stirling numbers). Let $$$(a_n)$$$ be a sequence and

$$$\displaystyle b_n = \sum_{k=1}^{n} S(n,k) a_k $$$

be is second-kind Stirling transform. Then

$$$\displaystyle a_n = \sum_{k=1}^{n} (-1)^{n-k} s(n,k) b_k. $$$

Proof

8 (Remark). I mentioned twice that this method can be generalised. For example, for the binomial transformation

$$$\displaystyle \{x_n\} \xrightarrow{\quad Binom\quad} \left\{ \sum_{k=0}^{n} \binom{n}{k} x_k \right\}, $$$

the main theorem will be the following

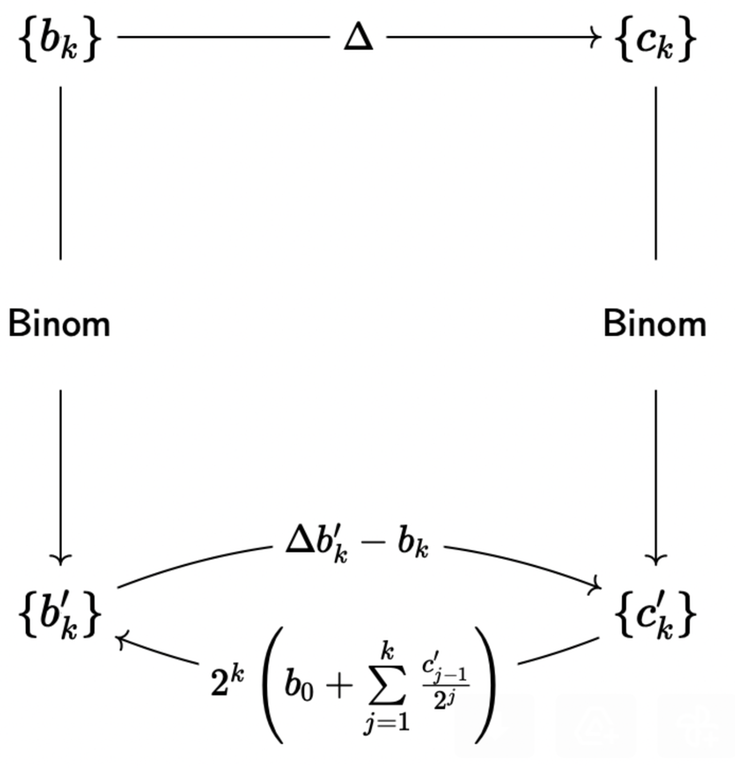
Using a similar strategy as in 6, we can prove that

$$$\displaystyle \sum_{n=0}^{N} \binom{N}{n} n^k = \sum_{j=0}^{k} S(k,j) \binom{n}{j} j! 2^{N-j}. $$$

History