1779A - Зал славы
Author: n0sk1ll
1779B - Конструктив от MKnez
1779C - Наименьшая префиксная сумма
Author: n0sk1ll
1779D - Борис и его восхитительная прическа
Author: n0sk1ll
1779B - Конструктив от MKnez
We will iterate over the array from right to left. Then, as described in the hint section, we will split the current $$$a_i$$$ and create almost equal parts. For example, $$$5$$$ split into three parts forms the subarray $$$[1,2,2]$$$. Splitting $$$8$$$ into four parts forms the subarray $$$[2,2,2,2]$$$. Notice that the subarrays must be sorted. Because we want to perform as few splits as possible, the rightmost endpoint value should be as high as possible (as long as it is lower than or equal to the leftmost endpoint of the splitting of $$$a_{i+1}$$$ if it exists).
When we iterate over the array, it is enough to set the current $$$a_i$$$ to the leftmost endpoint of the splitting (the smallest current value). It will help to calculate the optimal splitting of $$$a_{i-1}$$$. For the current $$$a_i$$$, we want to find the least $$$k$$$ such that we can split $$$a_{i-1}$$$ into $$$k$$$ parts so the rightmost endpoint is less than or equal to $$$a_i$$$. More formally, we want $$$\lceil \frac{a_{i-1}}{k} \rceil \leq a_i$$$ to hold. Afterwards, we set $$$a_{i-1}$$$ to $$$\lfloor \frac{a_{i-1}}{k} \rfloor$$$ and continue with our algorithm. The simplest way to find the desired $$$k$$$ is to apply the following formula:
The answer is the sum over all $$$k-1$$$.
There are $$$q \leq 2\cdot 10^5$$$ queries: given an index $$$i$$$ and an integer $$$x>1$$$, set $$$a_i := \lceil \frac{a_i}{x} \rceil$$$. Modify the array and print the answer to the original problem. Please note that the queries stack.
1779F - Ксолдовские камни
Author: n0sk1ll
To solve the problem for matrices of $$$3$$$-rd type, find the shortest path to $$$2$$$ closest exits with a modification of BFS. Block all cells not belonging to the path with obstacles.
For a matrix of type $$$1$$$, Misha can block all empty cells (except the one Vova stands on).
For a matrix of type $$$2$$$, Misha finds the shortest path to some exit with a single BFS and then blocks every other cell.
Matrices of type $$$3$$$ are more complicated. We want to find two shortest paths to the two closest exits and block the remaining empty cells.
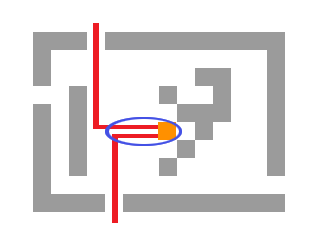
But, notice how the paths will likely share their beginnings. We do not have to count those cells twice. Let's take a look at the junction where the two paths merge. If we first fix the junction, finding the shortest path to Vova can be done by running a single BFS and precalculating the shortest distances from each cell to Vova. Finding the shortest path from the junction to the two closest exits can also be done with BFS and precalculation. We modify the BFS, making it multi-source, with a source in each exit. Also, we will allow each cell to be visited twice (but by different exits). We will need to maintain the following data for each cell:
- How many times was it visited;
- The last exit/source that visited it;
- The sum of paths from all exits/sources that visited the cell so far.
Running the BFS with proper implementation produces the answer. When everything said is precalculated, we fix the junction in $$$O(nm)$$$ ways (each empty cell can be a valid junction), and then calculate the shortest path from Vova to the two closest cells in $$$O(1)$$$ per junction.
Total complexity is $$$O(nm)$$$.
Solve the problem with LCA, or report that such solution does not exist.