Suppose you can only use $$$\texttt{U}$$$, $$$\texttt{R}$$$, $$$\texttt{D}$$$. Which cells can you reach?

If you only use buttons $$$\texttt{U}$$$, $$$\texttt{R}$$$, $$$\texttt{D}$$$, you can never reach the points with $$$x < 0$$$. However, if all the special points have $$$x \geq 0$$$, you can reach all of them with the following steps:

• visit all the special points with $$$x = 0$$$, using the buttons $$$\texttt{U}$$$, $$$\texttt{D}$$$;
• press the button $$$\texttt{R}$$$ to reach $$$x = 1$$$;
• visit all the special points with $$$x = 1$$$, using the buttons $$$\texttt{U}$$$, $$$\texttt{D}$$$;
• $$$\dots$$$
• visit all the special points with $$$x = 100$$$, using the buttons $$$\texttt{U}$$$, $$$\texttt{D}$$$.

Similarly, if you use at most $$$3$$$ buttons in total, you can reach all the special points if at least one of the following conditions is true:

• all $$$x_i \geq 0$$$;
• all $$$x_i \leq 0$$$;
• all $$$y_i \geq 0$$$;
• all $$$y_i \leq 0$$$.

Complexity: $$$O(n)$$$

Find a value of $$$k$$$ that works in many cases.

$$$k = 2$$$ works in many cases. What if it does not work?

If $$$k = 2$$$ does not work, either all the numbers are even or all the numbers are odd. Which $$$k$$$ can you try now?

Let $$$f(k)$$$ be the number of distinct values after the operation, using $$$k$$$.

Let's try $$$k = 2$$$. It works in all cases, except when either all the numbers are even or all the numbers are odd.

Let's generalize. If $$$a_i \text{ mod } k = x$$$, one of the following holds:

• $$$a_i \text{ mod } 2k = x$$$;
• $$$a_i \text{ mod } 2k = x+k$$$;

It means that, if $$$f(k) = 1$$$ (i.e., all the values after the operations are $$$x$$$), either $$$f(2k) = 1$$$ (if either all the values become $$$x$$$, or they all become $$$x+k$$$), or $$$f(2k) = 2$$$.

Therefore, it is sufficient to try $$$k = 2^1, \dots, 2^{57}$$$. In fact, $$$f(1) = 1$$$ and $$$f(2^{57}) = n$$$, so there must exist $$$m < 57$$$ such that $$$f(2^m) = 1$$$ and $$$f(2^{m+1}) \neq 1 \implies f(2^{m+1}) = 2$$$.

Alternative (more intuitive?) interpretation:

• $$$a_i \text{ mod } 2^j$$$ corresponds to the last $$$j$$$ digits in the binary representation of $$$a_i$$$. There must exist $$$j$$$ such that the last $$$j$$$ digits make exactly $$$2$$$ distinct blocks.

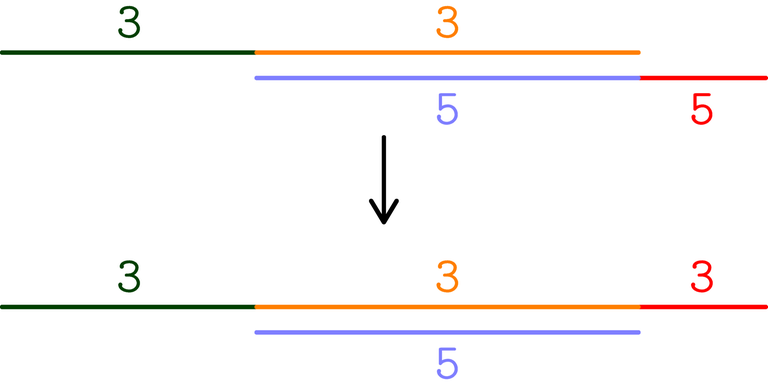
In the following picture, $$$a = [1005, 2005, 7005, 11005, 16005]$$$ and $$$k = 16$$$:

Complexity: $$$O(n \log(\max a_i))$$$

Assign bigger costs to shorter intervals.

Solve the problem with $$$n = 2$$$.

Solve the following case: $$$l = [1, 2]$$$, $$$r = [3, 4]$$$, $$$c = [1, 2]$$$. Can you generalize it?

You have to match each $$$l_i$$$ with some $$$r_j > l_i$$$.

Construct $$$v = {l_1, l_2, \dots, l_n, r_1, r_2, \dots, r_n}$$$ and sort it. If you replace every $$$l_i$$$ with the symbol $$$\texttt{(}$$$ and every $$$r_i$$$ with the symbol $$$\texttt{)}$$$, you get a regular bracket sequence (sketch of proof: $$$l_i < r_i$$$ for each $$$i$$$, so each prefix of symbols contains at least as many $$$\texttt{(}$$$ as $$$\texttt{)}$$$, so the bracket sequence is regular).

Now match each $$$\texttt{(}$$$ with the corresponding $$$\texttt{)}$$$. You can show that this is the optimal way to rearrange the $$$l_i$$$ and the $$$r_i$$$. (From now, let the $$$l_i$$$, $$$r_i$$$ and $$$c_i$$$ be the values after your rearrangement.)

Proof:

• If you match the brackets in any other way, you get two intervals such that their intersection is non-empty but it is different from both intervals (i.e., you get $$$l_i < l_j < r_i < r_j$$$).
• You have also assigned some cost $$$c_i$$$ to $$$[l_i, r_i]$$$ and $$$c_j$$$ to $$$[l_j, r_j]$$$. Without loss of generality, $$$c_i \leq c_j$$$ (the other case is symmetrical).
• If you swap $$$r_i$$$ and $$$r_j$$$, the cost does not increase.
• Repeat the process until you get the "regular" bracket matching. You can show that the process ends in a finite number of steps.

Now, you can get the minimum cost by sorting the intervals by increasing length and sorting the $$$c_i$$$ in decreasing order.

Alternative (more intuitive?) interpretation:

• If you solve the problem with $$$n = 2$$$ and try to generalize, you can notice that it seems optimal to match every $$$r_i$$$ with the largest unused $$$l_i$$$ (if you iterate over $$$r_i$$$ in increasing order).

You can implement the solution by using either a stack (to simulate the bracket matching) or a set (to find the largest unused $$$l_i$$$).

Complexity: $$$O(n \log n)$$$

Solve the problem with $$$k = 0$$$.

Solve the problem with generic $$$k$$$. When is the answer $$$-1$$$?

Do you notice any similarities between the cases with $$$k = 0$$$ and with generic $$$k$$$?

Consider the "shifted" problem, where each $$$x$$$ on the blackboard (at any moment) is replaced with $$$x' = x-k$$$.

Now, the operation becomes "replace $$$x$$$ with $$$y+z$$$ such that $$$x+y = z+k \implies (x'+k)+(y'+k) = (z'+k)+k \implies x'+y' = z'$$$". Therefore, in the shifted problem, $$$k' = 0$$$.

Now you can replace every $$$a'_i := a_i - k$$$ with any number of values with sum $$$a'_i$$$, and the answer is the amount of numbers on the blackboard at the end, minus $$$n$$$.

If we want to make all the values equal to $$$m'$$$, it must be a divisor of every $$$a'_i$$$.

• If all the $$$a'_i$$$ are positive, it is optimal to choose $$$m' = \gcd a'_i$$$.
• If all the $$$a'_i$$$ are zero, the answer is $$$0$$$.
• If all the $$$a'_i$$$ are negative, it is optimal to choose $$$m' = -\gcd -a'_i$$$.
• Otherwise, the answer is $$$-1$$$.

Alternative way to get this result:

• You have to split each $$$a_i$$$ into $$$p_i$$$ pieces equal to $$$m$$$, and their sum must be equal to $$$a_i + k(p_i - 1) = (a_i - k) + kp_i = mp_i$$$. Then, $$$(a_i - k) = (m - k)p_i$$$, so $$$m' = m-k$$$ must be a divisor of every $$$a'_i = a_i - k$$$.

In both the positive and the negative case, you will only write positive elements (in the original setup), as wanted.

• If all the $$$a'_i$$$ are positive, the numbers you will write on the shifted blackboard are positive, so they will be positive also in the original blackboard.
• If all the $$$a'_i$$$ are negative, the numbers you will write on the shifted blackboard are greater than the numbers you will erase, so they will be greater than the numbers in input (and positive) in the original blackboard.

Complexity: $$$O(n + \log(\max a_i))$$$

Find a strategy that turns "few" lamps on in most cases.

Pressing all the buttons turns $$$\lfloor \sqrt n \rfloor$$$ lamps on.

If the strategy in Hint 2 does not work, at most $$$3$$$ lamps must be on at the end.

Iterate over all subsets of at most $$$3$$$ lamps that must be on at the end.

If you press all the buttons, lamp $$$i$$$ is toggled by all the divisors of $$$i$$$, so it will be on if $$$i$$$ has an odd number of divisors, i.e., if $$$i$$$ is a perfect square.

Then, the strategy of pressing all the buttons works if $$$\lfloor \sqrt n \rfloor < \lfloor n/5 \rfloor$$$, which is true for $$$n \geq 20$$$.

If $$$n \leq 19$$$, at most $$$\lfloor 19/5 \rfloor = 3$$$ lamps must be turned on at the end.

If you know which lamps must be turned on at the end, you can iterate over the buttons from $$$1$$$ to $$$n$$$ and press button $$$i$$$ if and only if lamp $$$i$$$ is in the wrong state. So you can iterate over all subsets of at most $$$3$$$ lamps, and check if the corresponding choice of buttons is valid (i.e., the $$$m$$$ constraints hold). You can remove a $$$\log n$$$ factor by precalculating the choice of buttons for all small subsets before running the testcases.

Complexity for each test: $$$O((\sum n + \sum m) \cdot k^{2k-4})$$$ (if $$$\lfloor n/k \rfloor$$$ lamps must be on; in this case, $$$k = 5$$$).

Find a clean way to visualize the problem.

Draw a $$$n \times n$$$ grid, with tokens in $$$(i, p_i)$$$. Which constraints on the tokens do you have?

You have some "L" shapes, and each of them must contain a fixed number of tokens (in 1909F1 - Small Permutation Problem (Easy Version), the shapes are $$$1$$$ cell wide and must contain at most $$$2$$$ tokens). Iterate over the shapes in increasing order of $$$i$$$.

Split each shape into $$$2$$$ rectangles and iterate over the number of tokens in the first rectangle.

Draw a $$$n \times n$$$ grid, with tokens in $$$(i, p_i)$$$.

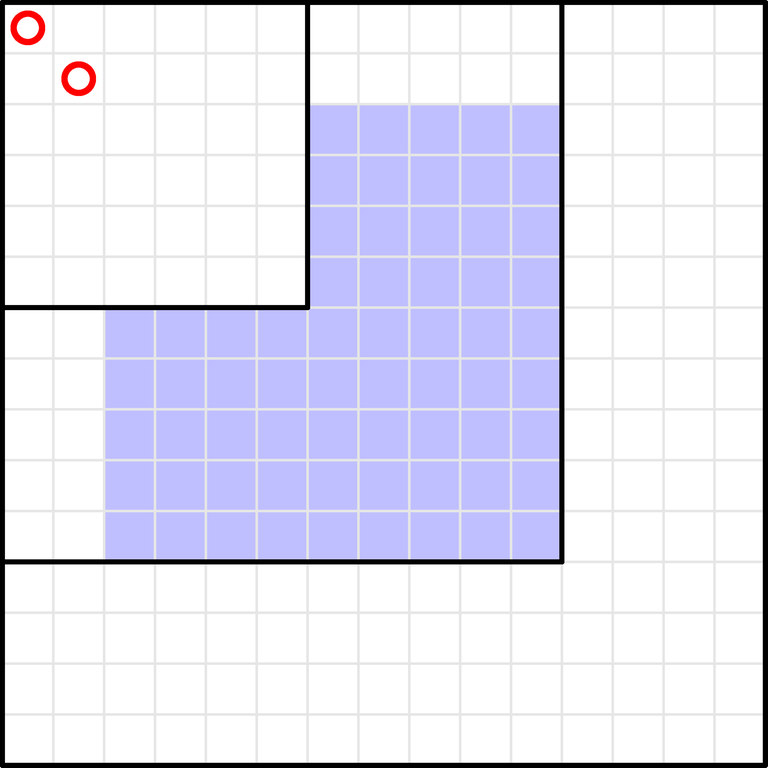
Consider any $$$a_i \neq -1$$$ and the nearest $$$a_j \neq -1$$$ on the left (if it does not exist, let's set $$$j = a_j = 0$$$). Then, there must be $$$a_i$$$ tokens in the subgrid $$$[1, i] \times [1, i]$$$. We can suppose we have already inserted the $$$a_j$$$ tokens in $$$[1, j] \times [1, j]$$$, and we have to insert $$$a_i - a_j$$$ tokens in the remaining cells of $$$[1, i] \times [1, i]$$$ (they make an "L" shape).

WLOG, the $$$a_j$$$ tokens in $$$[1, j] \times [1, j]$$$ are in the cells $$$(1, 1), \dots, (a_j, a_j)$$$. Then, we can put tokens in the blue cells in the picture.

The blue shape can be further split into these two rectangles:

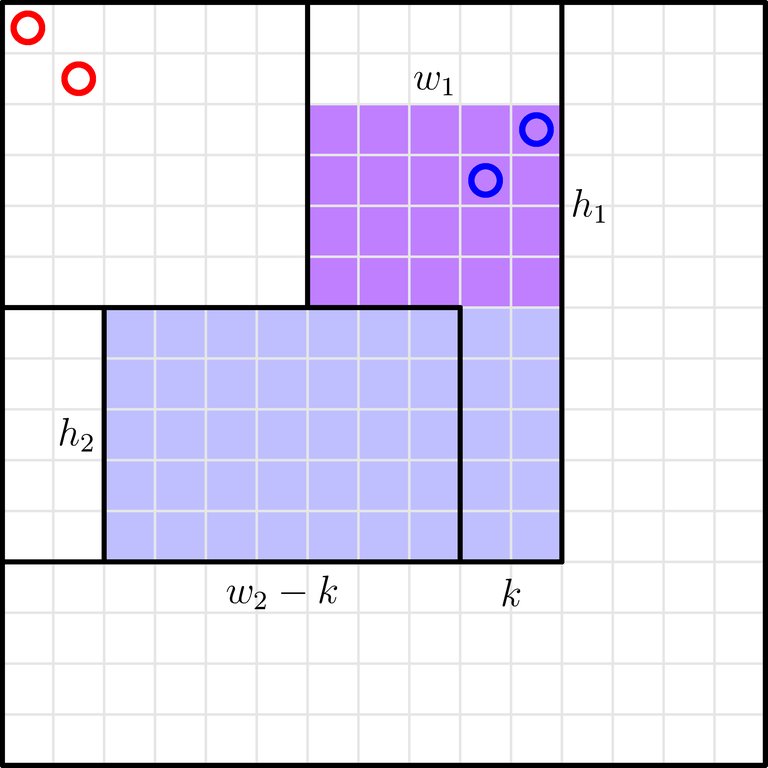
Iterate over $$$k$$$, the number of tokens in the first rectangle ($$$0 \leq k \leq a_i - a_j$$$). Then, you have to insert $$$k$$$ tokens into a $$$h_1 \times w_1$$$ rectangle, and the remaining $$$a_i - a_j - k$$$ tokens into a $$$h_2 \times (w_2 - k)$$$ rectangle.

The number of ways to insert $$$k$$$ tokens into a $$$h \times w$$$ rectangle is equal to the product of the number of ways to choose $$$k$$$ rows, the number of ways to choose $$$k$$$ columns, and the number of ways to fill the resulting $$$k \times k$$$ subgrid: the result is $$$\binom{h}{k} \binom{w}{k} k!$$$.

$$$a_n = n$$$ automatically (if $$$a_n \neq n$$$ and $$$a_n \neq -1$$$, the answer is $$$0$$$). If the non-negative $$$a_i$$$ are non-decreasing, the sum of the $$$a_i - a_j + 1$$$ (i.e., the $$$k$$$ over which you have to iterate) is $$$O(n)$$$, so the algorithm is efficient enough. Otherwise, the answer is $$$0$$$.

Complexity: $$$O(n)$$$

If you remove the condition $$$s = x+y+z$$$, the problem becomes harder.

Solve for a fixed $$$|y|$$$ (length of $$$y$$$).

Suppose you have found a valid $$$y$$$. Shift it one position to the right. When is it still valid?

The valid $$$y$$$ with $$$|y| = l$$$ start in consecutive positions.

Using the same idea of the proof of Hint 4, you can find all the valid $$$y$$$.

Let's use $$$s[l, r]$$$ to indicate the substring $$$[l, r]$$$ of $$$s$$$. Let's use $$$(a, b)$$$ to indicate the triple of strings $$$(s[1, a], s[a+1, b], s[b+1, n])$$$.

Suppose $$$(a, b)$$$ is valid. Then, $$$(a+1, b+1)$$$ is valid if and only if $$$s_{b+1} = t_{b+1}$$$.

If $$$(a, b)$$$ is valid, $$$s[1, b] = t[1, b]$$$; so if $$$s_b \neq t_b$$$, $$$(a+k, b+k)$$$ is invalid for $$$k \geq 0$$$. Therefore, if $$$(a, b)$$$ is the first valid pair with $$$b-a=l$$$ (i.e., with $$$|y| = l$$$), and $$$k$$$ is the smallest positive integer such that $$$(a+k, b+k)$$$ is invalid, then $$$s_{b+k} \neq t_{b+k}$$$, so the only valid pairs with $$$|y| = l$$$ are the $$$(a+j, b+j)$$$ with $$$0 \leq j < k$$$ (i.e., the valid $$$y$$$ with $$$|y| = l$$$ start in consecutive positions).

Now let's find all the valid $$$y$$$ with $$$|y| = l$$$. Suppose $$$(a, b)$$$ is valid, and $$$c$$$ is the minimum index such that $$$s_c \neq t_c$$$. Then, $$$b < r$$$, and $$$(a+k, b+k)$$$ is valid for all $$$b \leq b+k < c$$$. Similarly, if $$$d$$$ is the minimum integer such that $$$s_{n-d} \neq t_{m-d}$$$, $$$(a+k, b+k)$$$ is valid for all $$$n-d < a+k \leq a \implies n-d+l < b+k \leq b$$$.

Therefore, it's enough to check only one pair for each length, with $$$b$$$ in $$$[n-d+l+1, c-1]$$$ (because either all these pairs are valid or they are all invalid). This is possible by precomputing the rolling hash of the two strings. Alternatively, you can use z-function.

Complexity: $$$O(n)$$$

Find a strategy which is as simple and "easy to handle" as possible.

Only perform operations such that all swapped pairs have $$$a_i > a_{i+1}$$$. Let's call such subarrays "swappable".

First, for each $$$i$$$ from left to right, do the operation on $$$[j, i]$$$, where $$$j$$$ is the minimum index such that $$$[j, i]$$$ is swappable.

Repeat the same algorithm from right to left.

After Hints 3 and 4, the array is sorted. Prove it (it will be useful).

Assign $$$\texttt{B}$$$ to the indices $$$i$$$ such that $$$a_i < a_{i-1}$$$ and $$$\texttt{A}$$$ to the other indices. During the process in Hint 3, after the operation on index $$$i$$$, which properties do $$$\texttt{A}$$$, $$$\texttt{B}$$$ have in the prefix $$$[1, i]$$$?

Answer to Hint 6:

• the values of type $$$\texttt{A}$$$ are increasing;
• there are no two consecutive elements of type $$$\texttt{B}$$$.

The rest of the proof (i.e., what happens during the process in Hint 4) is relatively easy.

Now let's find an efficient implementation. We have to use the properties in Hint 7.

You have to find the longest $$$\texttt{AB} \dots \texttt{AB}$$$ ending in position $$$i$$$, and perform the operation on it. What happens during the operation?

$$$\texttt{A}$$$ will always remain $$$\texttt{A}$$$. For each $$$\texttt{B}$$$, you have to detect when it becomes $$$\texttt{A}$$$.

For each $$$\texttt{B}$$$, you can precompute the number of moves needed to make it $$$\texttt{A}$$$.

For example, you can use a segment tree with the following information: the type of each element, the positions of the elements of type $$$\texttt{B}$$$, and the number of moves required for each $$$\texttt{B}$$$ to become $$$\texttt{A}$$$.

Let's only perform operations such that all swapped pairs have $$$a_i > a_{i+1}$$$. Let's call such subarrays "swappable".

• First, for each $$$i$$$ from left to right, do the operation on $$$[j, i]$$$, where $$$j$$$ is the minimum index such that $$$[j, i]$$$ is swappable (let's call it "operation $$$1.i$$$").
• Then, for each $$$i$$$ from right to left, do the operation on $$$[j, i]$$$, where $$$j$$$ is the minimum index such that $$$[j, i]$$$ is swappable (let's call it "operation $$$2.i$$$").

After these operations, the array is sorted. Let's prove it.

Assign $$$\texttt{B}$$$ to the indices $$$i$$$ such that $$$a_i < a_{i-1}$$$ and $$$\texttt{A}$$$ to the other indices. After operation $$$1.i$$$, only assign letters in the prefix $$$[1, i]$$$ and ignore the other elements. During the operations $$$2.i$$$, assign letters to all the elements.

Most of the following proofs are by induction. After the operation $$$1.i$$$ (supposing the properties were true after the operation $$$1.(i-1)$$$):

• An element of type $$$\texttt{A}$$$ will always remain of type $$$\texttt{A}$$$. Proof: the only elements of type $$$\texttt{A}$$$ whose previous element changes are the ones in the subarray $$$[j, i]$$$, which are swapped with a smaller element of type $$$\texttt{B}$$$.
• There are no two consecutive elements of type $$$\texttt{B}$$$. Proof: if you swap $$$[j, i]$$$, $$$p_{j-1}$$$ (if it exists) must be of type $$$\texttt{A}$$$ (otherwise $$$[j-2, i]$$$ is swappable).
• The elements of type $$$\texttt{A}$$$ are increasing. Proof: it's true if no $$$\texttt{B}s$$$ become $$$\texttt{A}s$$$, and it's also true if some $$$\texttt{B}s$$$ become $$$\texttt{A}s$$$ because any of them is adjacent to two $$$\texttt{A}s$$$.

After the operation $$$2.i$$$:

• The three properties above are still true.
• The suffix $$$[i, n]$$$ contains the values in $$$[i, n]$$$ in order. Proof: $$$a_i$$$ is an $$$\texttt{A}$$$, so it must be the largest $$$p_i$$$ in $$$[1, i]$$$, which is $$$i$$$.

Now let's understand how we can implement the algorithm. Example implementation:

• We maintain a segment tree. The $$$i$$$-th position of the segment tree contains information about the element which was initially $$$p_i$$$. Note that the relative position of $$$\texttt{B}s$$$ never changes: for example, if you want information about the last $$$k$$$ $$$\texttt{B}s$$$ in the current permutation, and you search them in the segment tree, you will find exactly the last $$$k$$$ $$$\texttt{B}s$$$, even though their indices will not correspond to the current indices.
• We have to find the longest swappable subarray ending at $$$i$$$. It means we need the current positions of the $$$\texttt{B}s$$$. For each $$$\texttt{B}$$$ maintain the current position, and assume the position of all the $$$\texttt{A}s$$$ is $$$0$$$. Also maintain, for each element, if it is a $$$\texttt{B}$$$ or not. Note that the $$$\texttt{B}s$$$ that are affected by each operation can be found in a suffix of the segment tree.
• In this way, finding the longest swappable subarray can be done with a binary search on the segment tree: since $$$\texttt{B}s$$$ cannot be consecutive, you have to find the longest suffix such that the sum of the positions of the $$$\texttt{B}s$$$ is the maximum possible (i.e., if there are $$$k$$$ $$$\texttt{B}s$$$ and the last of them is in position $$$i$$$, the sum of their positions must be $$$k(i-k+1)$$$).
• After finding the longest subarray in the segment tree, you have to perform the operation on it, i.e., subtract $$$1$$$ from all the nonzero positions.
• Some $$$\texttt{B}s$$$ may become $$$\texttt{A}s$$$. How to detect them? Since $$$\texttt{A}s$$$ never become $$$\texttt{B}s$$$, a $$$\texttt{B}$$$ becomes $$$\texttt{A}$$$ after it is swapped with all the elements greater than it on its left. So you can precompute the number of swaps that every $$$\texttt{B}$$$ needs to become $$$\texttt{A}$$$, and put it in the segment tree as well. Again, the operation is "subtract $$$1$$$ from a range".
• Detecting $$$\texttt{A}s$$$ means detecting elements which need $$$0$$$ swaps to become $$$\texttt{A}s$$$. You can find them after each operation by traversing the segment tree (which must support "range min" on the number of swaps needed), and set their position to $$$0$$$ and the number of swaps needed to $$$\infty$$$.

Complexity: $$$2n-3$$$ moves, $$$O(n \log n)$$$ time.

Insert the elements into the permutation in some comfortable order.

Suppose $$$m$$$ is even. You can insert elements in the order $$$[m/2, m/2 - 1, m/2 + 1, m/2 - 2, \dots]$$$.

You can solve for a single $$$m$$$ with DP. Can you calculate the DP for multiple $$$m$$$ simultaneously?

The first part of the DP (where you insert both "small" and "big" elements) is the same for each $$$m$$$ (but with a different length), and for the second part (where you only insert "small" elements) you don't need DP.

The second part of the DP can be replaced with combinatorics formulas.

Binomials are compatible with NTT.

Let's solve for a single $$$m$$$. Suppose $$$m$$$ is even. Start from an empty array, and insert the elements in the order $$$[m/2, m/2 - 1, m/2 + 1, m/2 - 2, \dots]$$$. At any moment, all the elements are concatenated, and you can insert new elements either at the beginning, at the end or between two existing elements.

• When you insert an element $$$\geq m/2$$$, the sum with any of the previous inserted elements is $$$\geq m$$$.
• Otherwise, the sum is $$$< m$$$.

So you can calculate $$$dp_{i,j} =$$$ number of ways to insert the first $$$i$$$ elements (of $$$[m/2, m/2 - 1, m/2 + 1, m/2 - 2, \dots]$$$) and make $$$j$$$ "good" pairs (with sum $$$\geq m$$$).

You can split the ordering $$$[m/2, m/2 - 1, m/2 + 1, m/2 - 2, \dots]$$$ into two parts:

• small and big elements alternate;
• there are only small elements.

For the second part, you don't need DP. Suppose you have already inserted $$$i$$$ elements, and there are $$$j$$$ good pairs, but when you will have inserted all elements you want $$$k$$$ good pairs. The number of ways to insert the remaining elements can be computed with combinatorics in $$$O(1)$$$ after precomputing factorials and inverses (you have to choose which pairs to break and use stars and bars; we skip exact formulas because they are relatively easy to find).

If you rearrange the factorials correctly, you can get that all the answers for a fixed $$$m$$$ can be computed by multiplying two polynomials, one of which contains the $$$dp_{i,j}$$$, where $$$i$$$ is equal to the length of the "alternating" prefix. NTT is fast enough.

Complexity: $$$O(n^2 \log n)$$$