Heyo! If you tried to solve problem D you have probably ended up trying to optimize this algorithm:

    // input
    int n, k;
    cin >> n >> k;
    vector arr(n, vector<int>(n));
    for (int i = 0; i < n;i++)
        for (int j = i; j < n; j++)
            cin >> arr[i][j];

    vector dp(n+2, vector<int>());
    dp[n] = dp[n+1] = {0};

    for (int i = n-1; i >= 0; i--) {
        vector<int> cur;
        for (int j = i-1; j < n; j++) {
            // prepare to merge by adding a[i][j]
            vector<int> tomerge = dp[j+2];
            if (j >= i) {
                for (int& x : tomerge)
                    x += arr[i][j];
            }

            vector<int> merged;
            merge(cur.begin(), cur.end(),
                  tomerge.begin(), tomerge.end(),
                  back_inserter(merged), greater());
            cur = merged;
        }
        dp[i] = cur;
    }

    // output top k values
    for (int i = 0; i < k && i < dp[0].size(); i++)
        cout << dp[0][i] << ' ';
    cout << '\n';

But of course this won't work! The number of values in dp[i] will grow exponentially. But we only need to output first K values of the final dp[0]. Can we do better?

We only need to store first K values for each dp[i]. So we can rewrite: dp[i] = cur; while (dp[i].size() > k) dp[i].pop_back();

This leaves us with O(n^2 k) solution, this time the bottleneck is the merging part. The OFFICIAL solution is to use priority queue to select first K values after merging, without going through all values. But we are not interested in that!

LAZY solution

If you have heard about Haskell, you might know that it's a lazy language, it only computes things when it absolutely needs them -- e.g. when you print them. Could it be the case that just switching our programming language to Haskell make the solution pass? (Spoiler: yes, kindof)

Skeleton of Haskell code

{-# LANGUAGE BangPatterns #-}
{-# OPTIONS_GHC -O3 -optc-O3 -funbox-strict-fields -funfolding-use-threshold=16 #-}

import Control.Monad
import qualified Data.ByteString.Char8 as B
import Data.Maybe

import Data.Array.Unboxed
import Data.Array.IO.Safe
import Data.Array.IO.Internals

readInt = fst . fromJust . B.readInt
readInts = map readInt . B.words
putInts xs = do
  forM_ xs $ \x -> do
    B.putStr $$$ B.pack $$$ show x
    B.putStr $ B.pack " "
  B.putStr $ B.pack "\n"

main = do
  tests <- readInt <$> B.getLine
  replicateM_ tests solve

solve = do
  [n, k] <- readInts <$> B.getLine
  arrm <- newArray ((0, 0), (n-1, n-1)) 0 :: IO (IOUArray (Int, Int) Int)
  forM_ [0..n-1] $ \i -> do
    arrList <- readInts <$> B.getLine
    forM_ (zip arrList [i..n-1]) $ \(x, j) -> do
      writeArray arrm (i, j) x

  arr <- unsafeFreezeIOUArray arrm
  -- to be continued

Note: Codeforces is sometimes showing $$$' as '$$$$$, I don't know how to prevent that.

The code above reads the input into 2D array arr such that we can access element as arr ! (i, j).

Now we need the merge function, it takes 2 sorted lists and returns merged one:

merge :: [Int] -> [Int] -> [Int]
merge (x : xs) (y : ys) =
  if x > y
    then x : merge xs (y : ys)
    else y : merge (x : xs) ys
merge [] xs = xs
merge xs [] = xs

Pretty simple if you know the syntax, but it's not very important.

Now to rewrite the core of the algorithm above (it's possible to do this without recursion but it's less readable):

  let
    calc dp (-1) = head dp
    calc dp i = calc (curdp : dp) (i-1)
      where
        prepareMerge j dpval =
          if j < i then dpval
          else map (+ (arr ! (i, j))) dpval -- add arr[i][j] to every element
        tofold = zipWith prepareMerge [(i-1)..] dp
        curdp = ...
  putInts $$$ take k $$$ calc [[0], [0]] (n-1)

The base case is when i=-1, we just return dp[0]. dp stores the values of dp[i+1..n+1] for each iteration, instead of storing the full dp array. This better fits recursive implementation.

Where clause declares variables: tofold stores all the lists that we want to merge. Now consider:

curdp = foldr merge [] tofold

foldr function applies merge to every element from right to left:

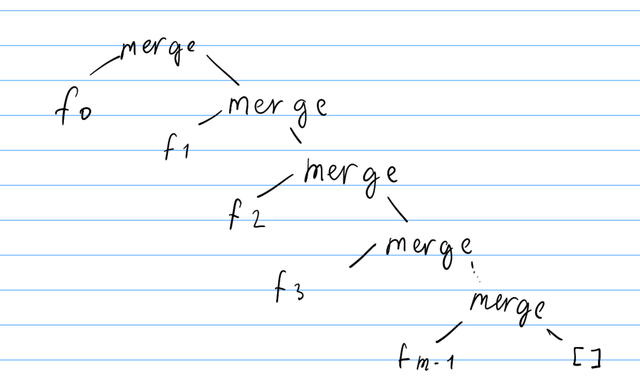
merge(tofold[0], merge(tofold[1], ... merge(tofold[m-1], [])))

Now our submission 254204408 confidently passes in 1300ms

How easy was that?

The catch

I have no idea how the above works. It should've worked in O(n*n*k) but it looks like working in O(n*n + k), maybe that's the editorial bonus solution?

Anyways, foldr version leads to this computation tree:

To get the first element of the array, Haskell might have to go through each merge node to find the smallest element. So the worst case for merging NxK arrays is O(nk), but if we use divide and conquer to merge the arrays:

mergeAll [] = []
mergeAll [arr] = arr
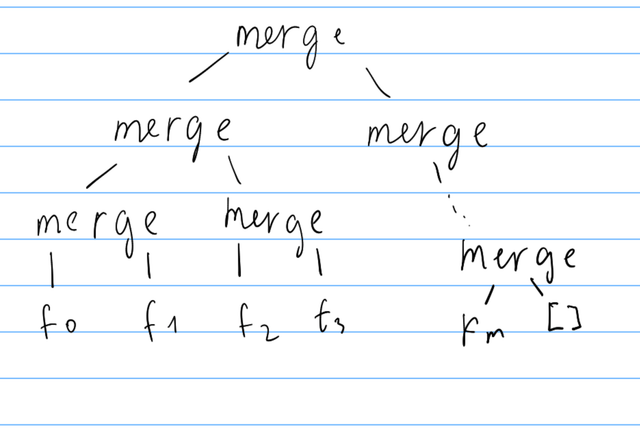
mergeAll arrs = merge (mergeAll (take mid arrs)) (mergeAll (drop mid arrs))
  where mid = length arrs `div` 2

This leads to this computation tree:

This way haskell will only have to go compare and go down O(log n) merge nodes to find the next smallest element. Now our submission 254204435 passes in 2500ms.

Python solution

If you look at Accepted python submissions to problem D you will see there are only 5 (!!) submissions. This is because python doesn't have builtin priority queue and writing PQ in python is very slow.

Adapting the lazy solution to python is possible by using half baked python feature called generators.

This is the submission 254208539 (...yeahhh.. merge function is very long in python). The foldr version is TLEing for some reason, I really have no idea how that passes in Haskell. The divide and conquer version passes in 4100ms. Note that we are using lazy only to merge the lists. We are using normal lists when storing them in dp[i]. This is because generators can be only consumed once in python, while Haskell lists act as both lazy lists and generators, depends on your view.

Conclusion

This was one of the coolist things I've done with Haskell (including outside of CP) and I wanted to share it :)