This is not a problem from any online judge, but for a project I am working on.↵
↵
There is an ellipse and a list of points. The task is to score the list with a number between $0$ and $1$. A score of $1$ means that the list of points forms a perfect ellipse. A list forms a perfect ellipse when:↵
↵
1. All the points in the list lie on the circumference of the ellipse.↵
↵
2. The points are evenly spaced (distributed evenly) across the circumference.↵
↵
<spoiler summary="Formal-ish statement">↵
You are given the center $(C_x, C_y)$ and the radii $(R_x, R_y)$ of an ellipse. You are also given a list $L$ of points, $(x_i, y_i)$ where $1\leq i\leq |L|$. You need to output the score of the list $L$ as described above.↵
</spoiler>↵
↵
The expected time complexity is less than $O(N^3)$, not strictly necessary.Here, $N$ is$N$ being the number of points in the list.↵
↵
If you want some inspiration, I have attempted the same problem but checked matching with circles and polygons. I am explaining how I did it for the circle.↵
↵
↵
↵
<spoiler summary="How it works">↵
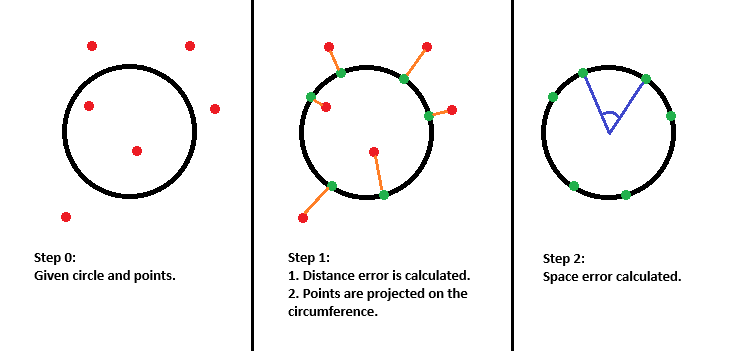
I determine the error instead of the score since it's easier, and do:↵
↵
$score = 1 - error$↵
↵
The error of a point is scored as a combination of two different errors.↵
↵
1. The distance error: How far a point is from the circumference.↵
↵
2. The space error: How far a point is from its neighbor from the expected distance.↵
↵
The space error is calculated between the projections of the point on the circumference to remove any distance bias it might have, since the distance error is handled differently.↵
↵
↵
↵
The root-mean square values of these errors are calculated and passed into a function, which returns a value $E$. There is a maximum tolerance value for the error $M$.↵
↵
The score is $1 -E/Mclamp(E/M, 0, 1)$.↵
</spoiler>↵
↵
↵
<spoiler summary="Code">↵
~~~~~↵
function get_projection_on_circumference(point) {↵
var angle = point_direction(center_x, center_y, point.x, point.y);↵
return new Point(↵
center_x + radius * cos(angle),↵
center_y + radius * sin(angle),↵
);↵
}↵
↵
function get_score(points) {↵
static max_error = 100;↵
var n_points = array_length(points);↵
↵
// error: distance from circumference↵
var dis_error = 0;↵
for (var i = 0; i < n_points; ++i) {↵
var point = points[i];↵
var dis = distance(center_x, center_y, point.x, point.y);↵
dis_error += sqr(radius - dis);↵
}↵
dis_error /= n_points;↵
dis_error = sqrt(dis_error);↵
↵
// project points on the circumference↵
for (var i = 0; i < n_points; ++i) {↵
points[i] = get_projection_on_circumference(points[i]);↵
}↵
↵
// sort "points" in anti-clockwise order↵
array_sort(points, function(p1, p2) {↵
var dir1 = point_direction(center_x, center_y, p1.x, p1.y);↵
var dir2 = point_direction(center_x, center_y, p2.x, p2.y);↵
return ((dir1 < dir2) ? -1 : 1);↵
});↵
↵
// error: evenly spaced↵
var space_error = 0;↵
var expected_angle = 360 / n_points;↵
var j = n_points-1;↵
for (var i = 0; i < n_points; ++i) {↵
var p1 = points[j];↵
var p2 = points[i];↵
var dis = distance(p1.x, p1.y, p2.x, p2.y);↵
var _val = clamp(1 - sqr(dis)/(2 * sqr(radius)), -1, 1);↵
var _angle = darccos(_val);↵
space_error += sqr(_angle - expected_angle);↵
j = i;↵
}↵
space_error /= n_points;↵
space_error = sqrt(space_error);↵
↵
// normalize error↵
var error = F(dis_error, space_error);↵
var error_normalized = clamp(error/max_error, 0, 1);↵
↵
// get score↵
return (1 - error_normalized);↵
}↵
~~~~~↵
</spoiler>↵
↵
You can see how the same method will work for regular polygons. For irregular (closed) polygons, I have a more sophisticated but similar way. The closed polygon method can work for ellipses (since an ellipse is actually a closed polygon with many small lines), but I am looking for a more natural solution for ellipses.
↵
There is an ellipse and a list of points. The task is to score the list with a number between $0$ and $1$. A score of $1$ means that the list of points forms a perfect ellipse. A list forms a perfect ellipse when:↵
↵
1. All the points in the list lie on the circumference of the ellipse.↵
↵
2. The points are evenly spaced (distributed evenly) across the circumference.↵
↵
<spoiler summary="Formal-ish statement">↵
You are given the center $(C_x, C_y)$ and the radii $(R_x, R_y)$ of an ellipse. You are also given a list $L$ of points, $(x_i, y_i)$ where $1\leq i\leq |L|$. You need to output the score of the list $L$ as described above.↵
</spoiler>↵
↵
The expected time complexity is less than $O(N^3)$, not strictly necessary.
↵
If you want some inspiration, I have attempted the same problem but checked matching with circles and polygons. I am explaining how I did it for the circle.↵
↵
↵
↵
<spoiler summary="How it works">↵
I determine the error instead of the score since it's easier, and do:↵
↵
$score = 1 - error$↵
↵
The error of a point is scored as a combination of two different errors.↵
↵
1. The distance error: How far a point is from the circumference.↵
↵
2. The space error: How far a point is from its neighbor from the expected distance.↵
↵
The space error is calculated between the projections of the point on the circumference to remove any distance bias it might have, since the distance error is handled differently.↵
↵
↵
↵
The root-mean square values of these errors are calculated and passed into a function, which returns a value $E$. There is a maximum tolerance value for the error $M$.↵
↵
The score is $1 -
</spoiler>↵
↵
↵
<spoiler summary="Code">↵
~~~~~↵
function get_projection_on_circumference(point) {↵
var angle = point_direction(center_x, center_y, point.x, point.y);↵
return new Point(↵
center_x + radius * cos(angle),↵
center_y + radius * sin(angle),↵
);↵
}↵
↵
function get_score(points) {↵
static max_error = 100;↵
var n_points = array_length(points);↵
↵
// error: distance from circumference↵
var dis_error = 0;↵
for (var i = 0; i < n_points; ++i) {↵
var point = points[i];↵
var dis = distance(center_x, center_y, point.x, point.y);↵
dis_error += sqr(radius - dis);↵
}↵
dis_error /= n_points;↵
dis_error = sqrt(dis_error);↵
↵
// project points on the circumference↵
for (var i = 0; i < n_points; ++i) {↵
points[i] = get_projection_on_circumference(points[i]);↵
}↵
↵
// sort "points" in anti-clockwise order↵
array_sort(points, function(p1, p2) {↵
var dir1 = point_direction(center_x, center_y, p1.x, p1.y);↵
var dir2 = point_direction(center_x, center_y, p2.x, p2.y);↵
return ((dir1 < dir2) ? -1 : 1);↵
});↵
↵
// error: evenly spaced↵
var space_error = 0;↵
var expected_angle = 360 / n_points;↵
var j = n_points-1;↵
for (var i = 0; i < n_points; ++i) {↵
var p1 = points[j];↵
var p2 = points[i];↵
var dis = distance(p1.x, p1.y, p2.x, p2.y);↵
var _val = clamp(1 - sqr(dis)/(2 * sqr(radius)), -1, 1);↵
var _angle = darccos(_val);↵
space_error += sqr(_angle - expected_angle);↵
j = i;↵
}↵
space_error /= n_points;↵
space_error = sqrt(space_error);↵
↵
// normalize error↵
var error = F(dis_error, space_error);↵
var error_normalized = clamp(error/max_error, 0, 1);↵
↵
// get score↵
return (1 - error_normalized);↵
}↵
~~~~~↵
</spoiler>↵
↵
You can see how the same method will work for regular polygons. For irregular (closed) polygons, I have a more sophisticated but similar way. The closed polygon method can work for ellipses (since an ellipse is actually a closed polygon with many small lines), but I am looking for a more natural solution for ellipses.





