This is not a problem from any online judge, but for a project I am working on.
There is an ellipse and a list of points. The task is to score the list with a number between $$$0$$$ and $$$1$$$. A score of $$$1$$$ means that the list of points forms a perfect ellipse. A list forms a perfect ellipse when:
All the points in the list lie on the circumference of the ellipse.
The points are evenly spaced (distributed evenly) across the circumference.
The expected time complexity is less than $$$O(N^3)$$$, not strictly necessary. $$$N$$$ being the number of points in the list.
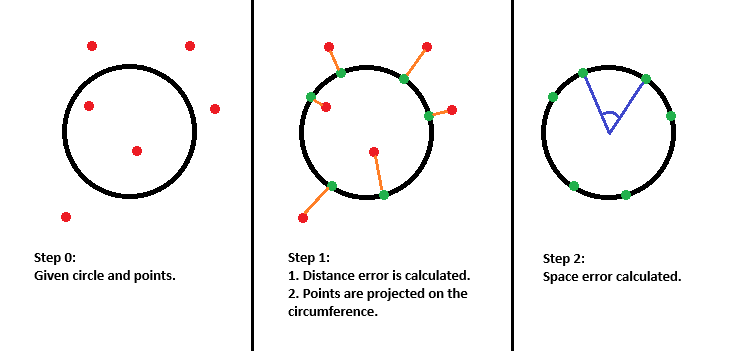
If you want some inspiration, I have attempted the same problem but checked matching with circles and polygons. I am explaining how I did it for the circle.
You can see how the same method will work for regular polygons. For irregular (closed) polygons, I have a more sophisticated but similar way. The closed polygon method can work for ellipses (since an ellipse is actually a closed polygon with many small lines), but I am looking for a more natural solution for ellipses.