| A | B | C | D | E | F | G | H | I | |
|---|---|---|---|---|---|---|---|---|---|
| Error_Yuan | 800 | 1200 | 1600 | 2100 | 2300 | 2600 | 3000 | 3400 | 3500 |
| sszcdjr | 800 | 1100 | 1600 | 2000 | 2300 | 2600 | 2900 | 3300 | 3500 |
| wyrqwq | 800 | 1000 | 1400 | 2200 | 2300 | 2600 | 3000 | 3500 | 3500 |
| Otomachi_Una | 800 | 1000 | 1600 | 2200 | 2400 | 2600 | 3200 | 3500 | 3500 |
| dXqwq | 900 | 1100 | 1700 | 2200 | 2400 | 2600 | 3200 | 3500 | 3500 |
| Kubic | 800 | 1000 | 1600 | 2400 | 2200 | 2800 | 3000 | 3500 | 3300 |
[problem:476175A]
Author: Otomachi_Una
Greedy from small to large.
We can delete the numbers from small to large. Thus, previously removed numbers will not affect future choices (if $$$x<y$$$, then $$$x$$$ cannot be a multiple of $$$y$$$). So an integer $$$x$$$ ($$$l\le x\le r$$$) can be removed if and only if $$$k\cdot x\le r$$$, that is, $$$x\le \left\lfloor\frac{r}{k}\right\rfloor$$$. The answer is $$$\max\left(\left\lfloor\frac{r}{k}\right\rfloor-l+1,0\right)$$$.
Time complexity: $$$\mathcal{O}(1)$$$ per test case.
#include <bits/stdc++.h>
#define all(s) s.begin(), s.end()
using namespace std;
using ll = long long;
using ull = unsigned long long;
const int _N = 1e5 + 5;
int T;
void solve() {
int l, r, k; cin >> l >> r >> k;
cout << max(r / k - l + 1, 0) << endl;
return;
}
int main() {
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
cin >> T;
while (T--) {
solve();
}
}
for _ in range(int(input())):
l, r, k = map(int, input().split())
print(max(r // k - l + 1, 0))
[problem:476175B]
Author: wyrqwq
($$$\texttt{01}$$$ or $$$\texttt{10}$$$ exists) $$$\Longleftrightarrow$$$ (both $$$\texttt{0}$$$ and $$$\texttt{1}$$$ exist).
Each time we do an operation, if $$$s$$$ consists only of $$$\texttt{0}$$$ or $$$\texttt{1}$$$, we surely cannot find any valid indices. Otherwise, we can always perform the operation successfully. In the $$$i$$$-th operation, if $$$t_i=\texttt{0}$$$, we actually decrease the number of $$$\texttt{1}$$$-s by $$$1$$$, and vice versa. Thus, we only need to maintain the number of $$$\texttt{0}$$$-s and $$$\texttt{1}$$$-s in $$$s$$$. If any of them falls to $$$0$$$ before the last operation, the answer is NO, otherwise, the answer is YES.
Time complexity: $$$\mathcal{O}(n)$$$ per test case.
#include <bits/stdc++.h>
#define all(s) s.begin(), s.end()
using namespace std;
using ll = long long;
const int _N = 1e5 + 5;
void solve() {
int n; cin >> n;
string s, t; cin >> s >> t;
int cnt0 = count(all(s), '0'), cnt1 = n - cnt0;
for (int i = 0; i < n - 1; i++) {
if (cnt0 == 0 || cnt1 == 0) {
cout << "NO" << '\n';
return;
}
if (t[i] == '1') cnt0--;
else cnt1--;
}
cout << "YES" << '\n';
}
int main() {
int T; cin >> T;
while (T--) {
solve();
}
}
for _ in range(int(input())):
n = int(input())
s = input()
one = s.count("1")
zero = s.count("0")
ans = "YES"
for ti in input():
if one == 0 or zero == 0:
ans = "NO"
break
one -= 1
zero -= 1
if ti == "1":
one += 1
else:
zero += 1
print(ans)
[problem:476175C]
Author: Error_Yuan
Binary search.
Do something backward.
First, do binary search on the answer. Suppose we're checking whether the answer can be $$$\ge k$$$ now.
Let $$$f_i$$$ be the current rating after participating in the $$$1$$$-st to the $$$i$$$-th contest (without skipping).
Let $$$g_i$$$ be the minimum rating before the $$$i$$$-th contest to make sure that the final rating is $$$\ge k$$$ (without skipping).
$$$f_i$$$-s can be calculated easily by simulating the process in the statement. For $$$g_i$$$-s, it can be shown that
where $$$g_{n+1}=k$$$.
Then, we should check if there exists an interval $$$[l,r]$$$ ($$$1\le l\le r\le n$$$), such that $$$f_{l-1}\ge g_{r+1}$$$. If so, we can choose to skip $$$[l,r]$$$ and get a rating of $$$\ge k$$$. Otherwise, it is impossible to make the rating $$$\ge k$$$.
We can enumerate on $$$r$$$ and use a prefix max to check whether valid $$$l$$$ exists.
Time complexity: $$$\mathcal{O}(n\log n)$$$ per test case.
Consider DP.
There are only three possible states for each contest: before, in, or after the skipped interval.
Consider $$$dp_{i,0/1/2}=$$$ the maximum rating after the $$$i$$$-th contest, where the $$$i$$$-th contest is before/in/after the skipped interval.
Let $$$f(a,x)=$$$ the result rating when current rating is $$$a$$$ and the performance rating is $$$x$$$, then
And the final answer is $$$\max(dp_{n,1}, dp_{n,2})$$$.
Time complexity: $$$\mathcal{O}(n)$$$ per test case.
#include <bits/stdc++.h>
#define all(s) s.begin(), s.end()
using namespace std;
using ll = long long;
using ull = unsigned long long;
const int _N = 1e5 + 5;
int T;
void solve() {
int n; cin >> n;
vector<int> a(n + 1);
for (int i = 1; i <= n; i++) cin >> a[i];
vector<int> pre(n + 1);
int curf = 0;
for (int i = 1; i <= n; i++) {
if (curf < a[i]) curf++;
else if (curf > a[i]) curf--;
pre[i] = max(pre[i - 1], curf);
}
auto check = [&](int k) {
int curg = k;
for (int i = n; i >= 1; i--) {
if (pre[i - 1] >= curg) return true;
if (a[i] < curg) curg++;
else curg--;
}
return false;
};
int L = 0, R = n + 1;
while (L < R) {
int mid = (L + R + 1) >> 1;
if (check(mid)) L = mid;
else R = mid - 1;
}
cout << L << '\n';
return;
}
int main() {
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
cin >> T;
while (T--) {
solve();
}
}
for _ in range(int(input())):
n = int(input())
def f(a, x):
return a + (a < x) - (a > x)
dp = [0, -n, -n]
for x in map(int, input().split()):
dp[2] = max(f(dp[1], x), f(dp[2], x))
dp[1] = max(dp[1], dp[0])
dp[0] = f(dp[0], x)
print(max(dp[1], dp[2]))
[problem:476175D]
Author: Error_Yuan
There are many different approaches to this problem. Only the easiest one (at least I think so) is shared here.
Try to make the graph into a forest first.
($$$deg_i\le 1$$$ for every $$$i$$$) $$$\Longrightarrow$$$ (The graph is a forest).
Let $$$d_i$$$ be the degree of vertex $$$i$$$.
First, we keep doing the following until it is impossible:
- Choose a vertex $$$u$$$ with $$$d_u\ge 2$$$, then find any two vertices $$$v,w$$$ adjacent to $$$u$$$. Perform the operation on $$$(u,v,w)$$$.
Since each operation decreases the number of edges by at least $$$1$$$, at most $$$m$$$ operations will be performed. After these operations, $$$d_i\le 1$$$ holds for every $$$i$$$. Thus, the resulting graph consists only of components with size $$$\le 2$$$.
If there are no edges, the graph is already cool, and we don't need to do any more operations.
Otherwise, let's pick an arbitrary edge $$$(u,v)$$$ as the base of the final tree, and then merge everything else to it.
For a component with size $$$=1$$$ (i.e. it is a single vertex $$$w$$$), perform the operation on $$$(u, v, w)$$$, and set $$$(u, v) \gets (u, w)$$$.
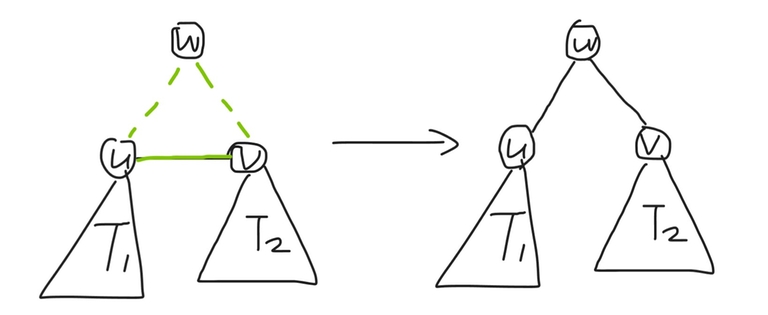
For a component with size $$$=2$$$ (i.e. it is an edge connecting $$$a$$$ and $$$b$$$), perform the operation on $$$(u, a, b)$$$.
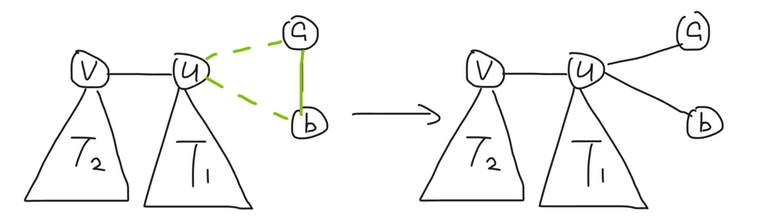
It is clear that the graph is transformed into a tree now.
In the author's solution, we used some data structures to maintain the edges, thus, the time complexity is $$$\mathcal{O}(n+m\log m)$$$ per test case.
#include <bits/stdc++.h>
using namespace std;
#ifdef DEBUG
#include "debug.hpp"
#else
#define debug(...) (void)0
#endif
using i64 = int64_t;
constexpr bool test = false;
int main() {
cin.tie(nullptr)->sync_with_stdio(false);
int t;
cin >> t;
for (int ti = 0; ti < t; ti += 1) {
int n, m;
cin >> n >> m;
vector<set<int>> adj(n + 1);
for (int i = 0, u, v; i < m; i += 1) {
cin >> u >> v;
adj[u].insert(v);
adj[v].insert(u);
}
vector<tuple<int, int, int>> ans;
for (int i = 1; i <= n; i += 1) {
while (adj[i].size() >= 2) {
int u = *adj[i].begin();
adj[i].erase(adj[i].begin());
int v = *adj[i].begin();
adj[i].erase(adj[i].begin());
adj[u].erase(i);
adj[v].erase(i);
ans.emplace_back(i, u, v);
if (adj[u].contains(v)) {
adj[u].erase(v);
adj[v].erase(u);
} else {
adj[u].insert(v);
adj[v].insert(u);
}
}
}
vector<int> s;
vector<pair<int, int>> p;
for (int i = 1; i <= n; i += 1) {
if (adj[i].size() == 0) {
s.push_back(i);
} else if (*adj[i].begin() > i) {
p.emplace_back(i, *adj[i].begin());
}
}
if (not p.empty()) {
auto [x, y] = p.back();
p.pop_back();
for (int u : s) {
ans.emplace_back(x, y, u);
tie(x, y) = pair(x, u);
}
for (auto [u, v] : p) {
ans.emplace_back(y, u, v);
}
}
println("{}", ans.size());
for (auto [x, y, z] : ans) println("{} {} {}", x, y, z);
}
}
[problem:476175E]
Author: Error_Yuan, wyrqwq
$$$2$$$ is powerful.
Consider primes.
How did you prove that $$$2$$$ can generate every integer except odd primes? Can you generalize it?
In this problem, we do not take the integer $$$1$$$ into consideration.
Claim 1. $$$2$$$ can generate every integer except odd primes.
Proof. For a certain non-prime $$$x$$$, let $$$\operatorname{mind}(x)$$$ be the minimum divisor of $$$x$$$. Then $$$x-\operatorname{mind}(x)$$$ must be an even number, which is $$$\ge 2$$$. So $$$x-\operatorname{mind}(x)$$$ can be generated by $$$2$$$, and $$$x$$$ can be generated by $$$x-\operatorname{mind}(x)$$$. Thus, $$$2$$$ is a generator of $$$x$$$.
Claim 2. Primes can only generated by themselves.
According to the above two claims, we can first check if there exist primes in the array $$$a$$$. If not, then $$$2$$$ is a common generator. Otherwise, let the prime be $$$p$$$, the only possible generator should be $$$p$$$ itself. So we only need to check whether $$$p$$$ is a generator of the rest integers.
For an even integer $$$x$$$, it is easy to see that, $$$p$$$ is a generator of $$$x$$$ if and only if $$$x\ge 2\cdot p$$$.
Claim 3. For a prime $$$p$$$ and an odd integer $$$x$$$, $$$p$$$ is a generator of $$$x$$$ if and only if $$$x - \operatorname{mind}(x)\ge 2\cdot p$$$.
Proof. First, $$$x-\operatorname{mind}(x)$$$ is the largest integer other than $$$x$$$ itself that can generate $$$x$$$. Moreover, only even numbers $$$\ge 2\cdot p$$$ can be generated by $$$p$$$ ($$$x-\operatorname{mind}(x)$$$ is even). That ends the proof.
Thus, we have found a good way to check if a certain number can be generated from $$$p$$$. We can use the linear sieve to pre-calculate all the $$$\operatorname{mind}(i)$$$-s.
Time complexity: $$$\mathcal{O}(\sum n+V)$$$, where $$$V=\max a_i$$$.
Some other solutions with worse time complexity can also pass, such as $$$\mathcal{O}(V\log V)$$$ and $$$\mathcal{O}(t\sqrt{V})$$$.
#include <bits/stdc++.h>
#define all(s) s.begin(), s.end()
using namespace std;
using ll = long long;
using ull = unsigned long long;
const int _N = 4e5 + 5;
int vis[_N], pr[_N], cnt = 0;
void init(int n) {
vis[1] = 1;
for (int i = 2; i <= n; i++) {
if (!vis[i]) {
pr[++cnt] = i;
}
for (int j = 1; j <= cnt && i * pr[j] <= n; j++) {
vis[i * pr[j]] = pr[j];
if (i % pr[j] == 0) continue;
}
}
}
int T;
void solve() {
int n; cin >> n;
vector<int> a(n + 1);
for (int i = 1; i <= n; i++) cin >> a[i];
int p = 0;
for (int i = 1; i <= n; i++) {
if (!vis[a[i]]) p = a[i];
}
if (!p) {
cout << 2 << '\n';
return;
}
for (int i = 1; i <= n; i++) {
if (a[i] == p) continue;
if (vis[a[i]] == 0) {
cout << -1 << '\n';
return;
}
if (a[i] & 1) {
if (a[i] - vis[a[i]] < 2 * p) {
cout << -1 << '\n';
return;
}
} else {
if (a[i] < 2 * p) {
cout << -1 << '\n';
return;
}
}
}
cout << p << '\n';
return;
}
int main() {
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
init(400000);
cin >> T;
while (T--) {
solve();
}
}
[problem:476175F]
Author: sszcdjr
If there are both consecutive $$$\texttt{R}$$$-s and $$$\texttt{B}$$$-s, does the condition hold for all $$$(i,j)$$$? Why?
Suppose that there are only consecutive $$$\texttt{R}$$$-s, check the parity of the number of $$$\texttt{R}$$$-s in each consecutive segment of $$$\texttt{R}$$$-s.
If for each consecutive segment of $$$\texttt{R}$$$-s, the parity of the number of $$$\texttt{R}$$$-s is odd, does the condition hold for all $$$(i,j)$$$? Why?
If for at least two of the consecutive segments of $$$\texttt{R}$$$-s, the parity of the number of $$$\texttt{R}$$$-s is even, does the condition hold for all $$$(i,j)$$$? Why?
Is this the necessary and sufficient condition? Why?
Don't forget some trivial cases like $$$\texttt{RRR...RB}$$$ and $$$\texttt{RRR...R}$$$.
For each $$$k>n$$$ or $$$k\leq0$$$, let $$$c_k$$$ be $$$c_{k\bmod n}$$$.
Lemma 1: If there are both consecutive $$$\texttt{R}$$$-s and $$$\texttt{B}$$$-s, the answer is \t{NO}.
Suppose that $$
#include <bits/stdc++.h>
using namespace std;
void solve(){
int n; cin>>n;
string s; cin>>s;
int visr=0,visb=0,ok=0;
for(int i=0;i<n;i++){
if(s[i]==s[(i+1)%n]){
if(s[i]=='R') visr=1;
else visb=1;
ok++;
}
}
if(visr&visb){
cout<<"NO\n";
return ;
}
if(ok==n){
cout<<"YES\n";
return ;
}
if(visb) for(int i=0;i<n;i++) s[i]='R'+'B'-s[i];
int st=0;
for(int i=0;i<n;i++) if(s[i]=='B') st=(i+1)%n;
vector<int> vc;
int ntot=0,cnt=0;
for(int i=0,j=st;i<n;i++,j=(j+1)%n){
if(s[j]=='B') vc.push_back(ntot),cnt+=(ntot&1)^1,ntot=0;
else ntot++;
}
if(vc.size()==1||cnt==1){
cout<<"YES\n";
return ;
}
cout<<"NO\n";
return ;
}
signed main(){
int t; cin>>t;
while(t--) solve();
return 0;
}
[problem:476175G]
Author: wyrqwq, Error_Yuan
This problem has two approaches. The first one is the authors' solution, and the second one was found during testing.
Coming soon.
Coming soon.
[problem:476175H]
Author: sszcdjr
It's hard to calculate the expected number. Try to change it to the probability.
Consider a $$$\mathcal{O}(3^n)$$$ dp first.
Use inclusion and exclusion.
Write out the transformation. Try to optimize it.
Let $$$dp_S$$$ be the probability such that exactly the points in $$$S$$$ has the message.
The answer is $$$\sum dp_S\cdot tr_S$$$, where $$$tr_S$$$ is the expected number of days before at least one vertex out of $$$S$$$ to have the message (counting from the day that exactly the points in $$$S$$$ has the message).
For transformation, enumerate $$$S,T$$$ such that $$$S\cap T=\varnothing$$$. Transfer $$$dp_S$$$ to $$$dp_{S\cup T}$$$. It's easy to precalculate the coefficient, and the time complexity differs from $$$\mathcal{O}(3^n)$$$, $$$\mathcal{O}(n\cdot 3^n)$$$ to $$$\mathcal{O}(n^2\cdot 3^n)$$$, according to the implementation.
The transformation is hard to optimize. Enumerate $$$T$$$ and calculate the probability such that vertices in $$$S$$$ is only connected with vertices in $$$T$$$, which means that the real status $$$R$$$ satisfies $$$S\subseteq R\subseteq (S\cup T)$$$. Use inclusion and exclusion to calculate the real probability.
List out the coefficient:
(Note that $$$w_e$$$ denotes the probability of the appearance of the edge $$$e$$$)
We can express it as $$$\mathrm{Const}\cdot f_{S\cup T}\cdot g_S\cdot h_T$$$. Use a subset convolution to optimize it. The total time complexity is $$$\mathcal{O}(2^n\cdot n^2)$$$.
It's easy to see that all $$$dp_S\neq0$$$ satisfies $$$1\in S$$$, so the time complexity can be $$$\mathcal{O}(2^{n-1}\cdot n^2)$$$ if well implemented.
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N=(1<<21),mod=998244353;
const int Lim=8e18;
inline void add(signed &i,int j){
i+=j;
if(i>=mod) i-=mod;
}
int qp(int a,int b){
int ans=1;
while(b){
if(b&1) (ans*=a)%=mod;
(a*=a)%=mod;
b>>=1;
}
return ans;
}
int dp[N],f[N],g[N],h[N];
int s1[N],s2[N];
signed pre[22][N/2],t[22][N/2],pdp[N][22];
int p[N],q[N],totp,totq;
signed main(){
int n,m; cin>>n>>m;
int totprod=1;
for(int i=0;i<(1<<n);i++) s1[i]=s2[i]=1;
for(int i=1;i<=m;i++){
int u,v,p,q; cin>>u>>v>>p>>q;
int w=p*qp(q,mod-2)%mod;
(s1[(1<<(u-1))+(1<<(v-1))]*=(mod+1-w))%=mod;
(s2[(1<<(u-1))+(1<<(v-1))]*=qp(mod+1-w,mod-2))%=mod;
(totprod*=(mod+1-w))%=mod;
}
for(int j=1;j<=n;j++) for(int i=0;i<(1<<n);i++) if((i>>(j-1))&1) (s1[i]*=s1[i^(1<<(j-1))])%=mod,(s2[i]*=s2[i^(1<<(j-1))])%=mod;
for(int i=0;i<(1<<n);i++) f[i]=s2[i],g[i]=totprod*s2[((1<<n)-1)^i]%mod*qp(mod+1-totprod*s2[i]%mod*s2[((1<<n)-1)^i]%mod,mod-2)%mod,h[i]=s1[i];
for(int i=1;i<(1<<n);i++) pre[__builtin_popcount(i)][i>>1]=h[i];
dp[1]=1;
for(int j=1;j<=n;j++){
if(!((1>>(j-1))&1)) add(pdp[1|(1<<(j-1))][j],mod-(dp[1]*g[1]%mod*f[1]%mod));
}
t[0][0]=dp[1]*g[1]%mod;
for(int k=1;k<=n;k++) for(int j=1;j<n;j++) for(int i=0;i<(1<<(n-1));i++) if((i>>(j-1))&1) add(pre[k][i],pre[k][i^(1<<(j-1))]);
for(int j=1;j<n;j++) for(int i=0;i<(1<<(n-1));i++) if((i>>(j-1))&1) add(t[0][i],t[0][i^(1<<(j-1))]);
for(int k=1;k<n;k++){
totp=totq=0;
for(int i=0;i<(1<<(n-1));i++) if(__builtin_popcount(i)<=k) p[++totp]=i; else q[++totq]=i;
for(int l=1,i=p[l];l<=totp;l++,i=p[l]) for(int j=0;j<k;j++) add(t[k][i],1ll*t[j][i]*pre[k-j][i]%mod);
for(int i=0;i<(1<<(n-1));i++) t[k][i]%=mod;
for(int j=1;j<n;j++) for(int l=1,i=p[l];l<=totp;l++,i=p[l]) if((i>>(j-1))&1) add(t[k][i],mod-t[k][i^(1<<(j-1))]);
for(int i=0;i<(1<<(n-1));i++){
if(__builtin_popcount(i)==k){
add(pdp[(i<<1)|1][0],t[k][i]*f[(i<<1)|1]%mod);
int pre=0;
for(int j=1;j<=n;j++){
(pre+=pdp[(i<<1)|1][j-1])%=mod;
if(!((((i<<1)|1)>>(j-1))&1)) add(pdp[(i<<1)|1|(1<<(j-1))][j],mod-pre);
}
(pre+=pdp[(i<<1)|1][n])%=mod;
dp[(i<<1)|1]=pre;
for(int j=1;j<=n;j++){
if(!((((i<<1)|1)>>(j-1))&1)) add(pdp[(i<<1)|1|(1<<(j-1))][j],mod-(dp[(i<<1)|1]*g[(i<<1)|1]%mod*f[(i<<1)|1]%mod));
}
t[k][i]=pre*g[(i<<1)|1]%mod;
}
else t[k][i]=0;
}
for(int j=1;j<n;j++) for(int l=1,i=q[l];l<=totq;l++,i=q[l]) if((i>>(j-1))&1) add(t[k][i],t[k][i^(1<<(j-1))]);
}
int ans=0;
for(int i=1;i<(1<<n)-1;i+=2) (ans+=dp[i]*qp(mod+1-totprod*s2[i]%mod*s2[((1<<n)-1)^i]%mod,mod-2)%mod)%=mod;
cout<<ans;
return 0;
}
[problem:476175I]
Author: Error_Yuan
The intended solution has nothing to do with dynamic programming.
This is the key observation to the problem. Suppose we have an array $$$b$$$ and a function $$$f(x)=\sum (b_i-x)^2$$$, then the minimum value of $$$f(x)$$$ is the variance of $$$b$$$.
Using the observation mentioned in Hint 2, we can reduce the problem to minimizing $$$\sum(a_i-x)^2$$$ for a given $$$x$$$. There are only $$$\mathcal{O}(n\cdot m)$$$ possible $$$x$$$-s.
The rest of the problem is way easy. Try flows, or just find a greedy algorithm!
If you are trying flows: the quadratic function is always convex.
Key Observation. Suppose we have an array $$$b$$$ and a function $$$f(x)=\sum (b_i-x)^2$$$, then the minimum value of $$$f(x)$$$ is the variance of $$$b$$$.
Proof. This is a quadratic function of $$$x$$$, and the its symmetry axis is $$$x=\frac{1}{n}\sum b_i$$$. So the minimum value is $$$f\left(\frac{1}{n}\sum b_i\right)$$$. That is exactly the definition of variance.
Thus, we can enumerate all possible $$$x$$$-s, and find the minimum $$$\sum (a_i-x)^2$$$ after the operations, then take the minimum accross them. That will give the correct answer to the original problem. Note that there are only $$$\mathcal{O}(n\cdot m)$$$ possible $$$x$$$-s.
More formally, let $$$k_{x,c}$$$ be the minimum value of $$$\sum (a_i-x)^2$$$ after exactly $$$c$$$ operations. Then $$$\mathrm{ans}_i=\displaystyle\min_{\text{any possible }x} k_{x,i}$$$.
So we only need to solve the following (reduced) problem:
- Given an (maybe non-integer) number $$$x$$$. For each $$$1\le i\le m$$$, find the minimum value of $$$\sum (a_i-x)^2$$$ after exactly $$$i$$$ operations.
To solve this, we can use the MCMF model:
- Set a source node $$$s$$$ and a target node $$$t$$$.
- For each $$$1\le i\le n$$$, add an edge from $$$s$$$ to $$$i$$$ with cost $$$0$$$.
- For each $$$1\le i\le n$$$, add an edge from $$$i$$$ to $$$t$$$ with cost $$$0$$$.
- For each $$$1\le i< n$$$, add an edge from $$$i$$$ to $$$i+1$$$ with cost being a function $$$\mathrm{cost}(f)=(a_i+f-x)^2-(a_i-x)^2$$$, where $$$f$$$ is the flow on this edge.
- Note that the $$$\mathrm{cost}$$$ function is convex, so this model is correct, as you can split an edge into some edges with cost of $$$\mathrm{cost}(1)$$$, $$$\mathrm{cost}(2)-\mathrm{cost}(1)$$$, $$$\mathrm{cost}(3)-\mathrm{cost}(2)$$$, and so on.
Take a look at the model again. We don't need to run MCMF actually. We can see that it is just a process of regret greedy. So you only need to find the LIS (Largest Interval Sum :) ) for each operation.
Thus, we solved the reduced problem in $$$\mathcal{O(n\cdot m)}$$$.
Overall time complexity: $$$\mathcal{O}((n\cdot m)^2)$$$ per test case.
Reminder: don't forget to use __int128 if you didn't handle the numbers carefully!
#include <bits/stdc++.h>
#define all(s) s.begin(), s.end()
using namespace std;
using ll = long long;
using ull = unsigned long long;
const int _N = 1e5 + 5;
int T;
void solve() {
ll n, m, k; cin >> n >> m >> k;
vector<ll> a(n + 1);
for (int i = 1; i <= n; i++) cin >> a[i];
vector<ll> kans(m + 1, LLONG_MAX);
vector<__int128> f(n + 1), g(n + 1), v(n + 1);
vector<int> vis(n + 1), L(n + 1), L2(n + 1);
ll sum = 0;
for (int i = 1; i <= n; i++) sum += a[i];
__int128 pans = 0;
for (int i = 1; i <= n; i++) pans += n * a[i] * a[i];
auto work = [&](ll s) {
__int128 ans = pans;
ans += s * s - 2ll * sum * s;
f.assign(n + 1, LLONG_MAX);
g.assign(n + 1, LLONG_MAX);
for (int i = 1; i <= n; i++) {
v[i] = n * (2 * a[i] * k + k * k) - 2ll * s * k;
vis[i] = 0;
}
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
L[j] = L2[j] = j;
if (f[j - 1] < 0) f[j] = f[j - 1] + v[j], L[j] = L[j - 1];
else f[j] = v[j];
if (!vis[j]) {
g[j] = LLONG_MAX;
continue;
}
if (g[j - 1] < 0) g[j] = g[j - 1] + 2ll * n * k * k - v[j], L2[j] = L2[j - 1];
else g[j] = 2ll * n * k * k - v[j];
}
__int128 min_sum = LLONG_MAX;
int l = 1, r = n, type = 0;
for (int j = 1; j <= n; j++) {
if (f[j] < min_sum) {
min_sum = f[j], r = j, l = L[j];
}
}
for (int j = 1; j <= n; j++) {
if (g[j] < min_sum) {
min_sum = g[j], r = j, l = L2[j];
type = 1;
}
}
ans += min_sum;
if (type == 0) {
for (int j = l; j <= r; j++) vis[j]++, v[j] += 2 * n * k * k;
} else {
for (int j = l; j <= r; j++) vis[j]--, v[j] -= 2 * n * k * k;
}
kans[i] = min((__int128)kans[i], ans);
}
};
for (ll x = sum; x <= sum + n * m * k; x += k) {
work(x);
}
for (int i = 1; i <= m; i++) cout << kans[i] << " \n"[i == m];
return;
}
int main() {
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
cin >> T;
while (T--) {
solve();
}
}





