| A | B | C | D | E | F | G | H | I | |
|---|---|---|---|---|---|---|---|---|---|
| Error_Yuan | 800 | 1200 | 1600 | 2100 | 2300 | 2600 | 3000 | 3400 | 3500 |
| sszcdjr | 800 | 1100 | 1600 | 2000 | 2300 | 2600 | 2900 | 3300 | 3500 |
| _istil | 800 | 1000 | 1400 | 2200 | 2300 | 2600 | 3000 | 3500 | 3500 |
| Otomachi_Una | 800 | 1000 | 1600 | 2200 | 2400 | 2600 | 3200 | 3500 | 3500 |
| dXqwq | 900 | 1100 | 1700 | 2200 | 2400 | 2600 | 3200 | 3500 | 3500 |
| Kubic | 800 | 1000 | 1600 | 2400 | 2200 | 2800 | 3000 | 3500 | 3300 |
[problem:476175A]
Author: Otomachi_Una
Greedy from small to large.
We can delete the numbers from small to large. Thus, previously removed numbers will not affect future choices (if $$$x<y$$$, then $$$x$$$ cannot be a multiple of $$$y$$$). So an integer $$$x$$$ ($$$l\le x\le r$$$) can be removed if and only if $$$k\cdot x\le r$$$, that is, $$$x\le \left\lfloor\frac{r}{k}\right\rfloor$$$. The answer is $$$\max\left(\left\lfloor\frac{r}{k}\right\rfloor-l+1,0\right)$$$.
Time complexity: $$$\mathcal{O}(1)$$$ per test case.
#include <bits/stdc++.h>
#define all(s) s.begin(), s.end()
using namespace std;
using ll = long long;
using ull = unsigned long long;
const int _N = 1e5 + 5;
int T;
void solve() {
int l, r, k; cin >> l >> r >> k;
cout << max(r / k - l + 1, 0) << endl;
return;
}
int main() {
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
cin >> T;
while (T--) {
solve();
}
}
for _ in range(int(input())):
l, r, k = map(int, input().split())
print(max(r // k - l + 1, 0))
[problem:476175B]
Author: _istil
($$$\texttt{01}$$$ or $$$\texttt{10}$$$ exists) $$$\Longleftrightarrow$$$ (both $$$\texttt{0}$$$ and $$$\texttt{1}$$$ exist).
Each time we do an operation, if $$$s$$$ consists only of $$$\texttt{0}$$$ or $$$\texttt{1}$$$, we surely cannot find any valid indices. Otherwise, we can always perform the operation successfully. In the $$$i$$$-th operation, if $$$t_i=\texttt{0}$$$, we actually decrease the number of $$$\texttt{1}$$$-s by $$$1$$$, and vice versa. Thus, we only need to maintain the number of $$$\texttt{0}$$$-s and $$$\texttt{1}$$$-s in $$$s$$$. If any of them falls to $$$0$$$ before the last operation, the answer is NO, otherwise, the answer is YES.
Time complexity: $$$\mathcal{O}(n)$$$ per test case.
#include <bits/stdc++.h>
#define all(s) s.begin(), s.end()
using namespace std;
using ll = long long;
const int _N = 1e5 + 5;
void solve() {
int n; cin >> n;
string s, t; cin >> s >> t;
int cnt0 = count(all(s), '0'), cnt1 = n - cnt0;
for (int i = 0; i < n - 1; i++) {
if (cnt0 == 0 || cnt1 == 0) {
cout << "NO" << '\n';
return;
}
if (t[i] == '1') cnt0--;
else cnt1--;
}
cout << "YES" << '\n';
}
int main() {
int T; cin >> T;
while (T--) {
solve();
}
}
for _ in range(int(input())):
n = int(input())
s = input()
one = s.count("1")
zero = s.count("0")
ans = "YES"
for ti in input():
if one == 0 or zero == 0:
ans = "NO"
break
one -= 1
zero -= 1
if ti == "1":
one += 1
else:
zero += 1
print(ans)
[problem:476175C]
Author: Error_Yuan
Binary search.
Do something backward.
First, do binary search on the answer. Suppose we're checking whether the answer can be $$$\ge k$$$ now.
Let $$$f_i$$$ be the current rating after participating in the $$$1$$$-st to the $$$i$$$-th contest (without skipping).
Let $$$g_i$$$ be the minimum rating before the $$$i$$$-th contest to make sure that the final rating is $$$\ge k$$$ (without skipping).
$$$f_i$$$-s can be calculated easily by simulating the process in the statement. For $$$g_i$$$-s, it can be shown that
where $$$g_{n+1}=k$$$.
Then, we should check if there exists an interval $$$[l,r]$$$ ($$$1\le l\le r\le n$$$), such that $$$f_{l-1}\ge g_{r+1}$$$. If so, we can choose to skip $$$[l,r]$$$ and get a rating of $$$\ge k$$$. Otherwise, it is impossible to make the rating $$$\ge k$$$.
We can enumerate on $$$r$$$ and use a prefix max to check whether valid $$$l$$$ exists.
Time complexity: $$$\mathcal{O}(n\log n)$$$ per test case.
Consider DP.
There are only three possible states for each contest: before, in, or after the skipped interval.
Consider $$$dp_{i,0/1/2}=$$$ the maximum rating after the $$$i$$$-th contest, where the $$$i$$$-th contest is before/in/after the skipped interval.
Let $$$f(a,x)=$$$ the result rating when current rating is $$$a$$$ and the performance rating is $$$x$$$, then
And the final answer is $$$\max(dp_{n,1}, dp_{n,2})$$$.
Time complexity: $$$\mathcal{O}(n)$$$ per test case.
#include <bits/stdc++.h>
#define all(s) s.begin(), s.end()
using namespace std;
using ll = long long;
using ull = unsigned long long;
const int _N = 1e5 + 5;
int T;
void solve() {
int n; cin >> n;
vector<int> a(n + 1);
for (int i = 1; i <= n; i++) cin >> a[i];
vector<int> pre(n + 1);
int curf = 0;
for (int i = 1; i <= n; i++) {
if (curf < a[i]) curf++;
else if (curf > a[i]) curf--;
pre[i] = max(pre[i - 1], curf);
}
auto check = [&](int k) {
int curg = k;
for (int i = n; i >= 1; i--) {
if (pre[i - 1] >= curg) return true;
if (a[i] < curg) curg++;
else curg--;
}
return false;
};
int L = 0, R = n + 1;
while (L < R) {
int mid = (L + R + 1) >> 1;
if (check(mid)) L = mid;
else R = mid - 1;
}
cout << L << '\n';
return;
}
int main() {
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
cin >> T;
while (T--) {
solve();
}
}
for _ in range(int(input())):
n = int(input())
def f(a, x):
return a + (a < x) - (a > x)
dp = [0, -n, -n]
for x in map(int, input().split()):
dp[2] = max(f(dp[1], x), f(dp[2], x))
dp[1] = max(dp[1], dp[0])
dp[0] = f(dp[0], x)
print(max(dp[1], dp[2]))
[problem:476175D]
Author: Error_Yuan
There are many different approaches to this problem. Only the easiest one (at least I think so) is shared here.
Try to make the graph into a forest first.
($$$deg_i\le 1$$$ for every $$$i$$$) $$$\Longrightarrow$$$ (The graph is a forest).
Let $$$d_i$$$ be the degree of vertex $$$i$$$.
First, we keep doing the following until it is impossible:
- Choose a vertex $$$u$$$ with $$$d_u\ge 2$$$, then find any two vertices $$$v,w$$$ adjacent to $$$u$$$. Perform the operation on $$$(u,v,w)$$$.
Since each operation decreases the number of edges by at least $$$1$$$, at most $$$m$$$ operations will be performed. After these operations, $$$d_i\le 1$$$ holds for every $$$i$$$. Thus, the resulting graph consists only of components with size $$$\le 2$$$.
If there are no edges, the graph is already cool, and we don't need to do any more operations.
Otherwise, let's pick an arbitrary edge $$$(u,v)$$$ as the base of the final tree, and then merge everything else to it.
For a component with size $$$=1$$$ (i.e. it is a single vertex $$$w$$$), perform the operation on $$$(u, v, w)$$$, and set $$$(u, v) \gets (u, w)$$$.
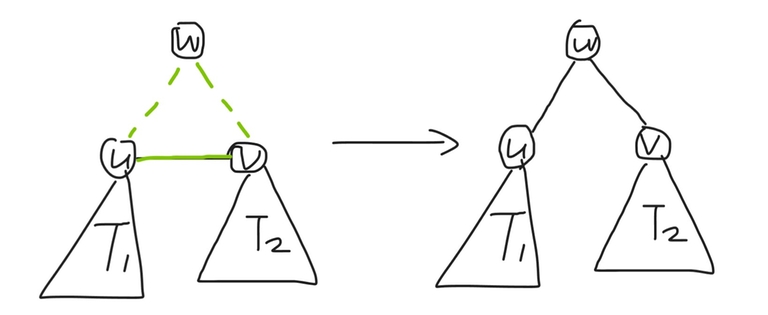
For a component with size $$$=2$$$ (i.e. it is an edge connecting $$$a$$$ and $$$b$$$), perform the operation on $$$(u, a, b)$$$.
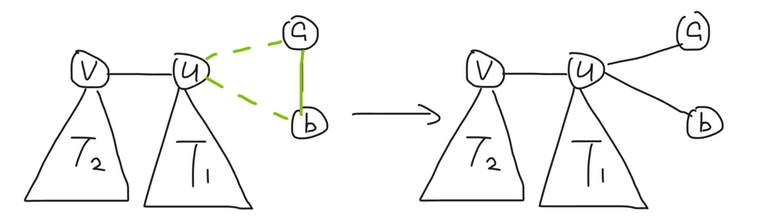
It is clear that the graph is transformed into a tree now.
In the author's solution, we used some data structures to maintain the edges, thus, the time complexity is $$$\mathcal{O}(n+m\log m)$$$ per test case.
#include <bits/stdc++.h>
using namespace std;
#ifdef DEBUG
#include "debug.hpp"
#else
#define debug(...) (void)0
#endif
using i64 = int64_t;
constexpr bool test = false;
int main() {
cin.tie(nullptr)->sync_with_stdio(false);
int t;
cin >> t;
for (int ti = 0; ti < t; ti += 1) {
int n, m;
cin >> n >> m;
vector<set<int>> adj(n + 1);
for (int i = 0, u, v; i < m; i += 1) {
cin >> u >> v;
adj[u].insert(v);
adj[v].insert(u);
}
vector<tuple<int, int, int>> ans;
for (int i = 1; i <= n; i += 1) {
while (adj[i].size() >= 2) {
int u = *adj[i].begin();
adj[i].erase(adj[i].begin());
int v = *adj[i].begin();
adj[i].erase(adj[i].begin());
adj[u].erase(i);
adj[v].erase(i);
ans.emplace_back(i, u, v);
if (adj[u].contains(v)) {
adj[u].erase(v);
adj[v].erase(u);
} else {
adj[u].insert(v);
adj[v].insert(u);
}
}
}
vector<int> s;
vector<pair<int, int>> p;
for (int i = 1; i <= n; i += 1) {
if (adj[i].size() == 0) {
s.push_back(i);
} else if (*adj[i].begin() > i) {
p.emplace_back(i, *adj[i].begin());
}
}
if (not p.empty()) {
auto [x, y] = p.back();
p.pop_back();
for (int u : s) {
ans.emplace_back(x, y, u);
tie(x, y) = pair(x, u);
}
for (auto [u, v] : p) {
ans.emplace_back(y, u, v);
}
}
println("{}", ans.size());
for (auto [x, y, z] : ans) println("{} {} {}", x, y, z);
}
}
[problem:476175E]
Author: Error_Yuan, _istil
$$$2$$$ is powerful.
Consider primes.
How did you prove that $$$2$$$ can generate every integer except odd primes? Can you generalize it?
In this problem, we do not take the integer $$$1$$$ into consideration.
Claim 1. $$$2$$$ can generate every integer except odd primes.
Proof. For a certain non-prime $$$x$$$, let $$$\operatorname{mind}(x)$$$ be the minimum divisor of $$$x$$$. Then $$$x-\operatorname{mind}(x)$$$ must be an even number, which is $$$\ge 2$$$. So $$$x-\operatorname{mind}(x)$$$ can be generated by $$$2$$$, and $$$x$$$ can be generated by $$$x-\operatorname{mind}(x)$$$. Thus, $$$2$$$ is a generator of $$$x$$$.
Claim 2. Primes can only generated by themselves.
According to the above two claims, we can first check if there exist primes in the array $$$a$$$. If not, then $$$2$$$ is a common generator. Otherwise, let the prime be $$$p$$$, the only possible generator should be $$$p$$$ itself. So we only need to check whether $$$p$$$ is a generator of the rest integers.
For an even integer $$$x$$$, it is easy to see that, $$$p$$$ is a generator of $$$x$$$ if and only if $$$x\ge 2\cdot p$$$.
Claim 3. For a prime $$$p$$$ and an odd integer $$$x$$$, $$$p$$$ is a generator of $$$x$$$ if and only if $$$x - \operatorname{mind}(x)\ge 2\cdot p$$$.
Proof. First, $$$x-\operatorname{mind}(x)$$$ is the largest integer other than $$$x$$$ itself that can generate $$$x$$$. Moreover, only even numbers $$$\ge 2\cdot p$$$ can be generated by $$$p$$$ ($$$x-\operatorname{mind}(x)$$$ is even). That ends the proof.
Thus, we have found a good way to check if a certain number can be generated from $$$p$$$. We can use the linear sieve to pre-calculate all the $$$\operatorname{mind}(i)$$$-s.
Time complexity: $$$\mathcal{O}(\sum n+V)$$$, where $$$V=\max a_i$$$.
Some other solutions with worse time complexity can also pass, such as $$$\mathcal{O}(V\log V)$$$ and $$$\mathcal{O}(t\sqrt{V})$$$.
#include <bits/stdc++.h>
#define all(s) s.begin(), s.end()
using namespace std;
using ll = long long;
using ull = unsigned long long;
const int _N = 4e5 + 5;
int vis[_N], pr[_N], cnt = 0;
void init(int n) {
vis[1] = 1;
for (int i = 2; i <= n; i++) {
if (!vis[i]) {
pr[++cnt] = i;
}
for (int j = 1; j <= cnt && i * pr[j] <= n; j++) {
vis[i * pr[j]] = pr[j];
if (i % pr[j] == 0) continue;
}
}
}
int T;
void solve() {
int n; cin >> n;
vector<int> a(n + 1);
for (int i = 1; i <= n; i++) cin >> a[i];
int p = 0;
for (int i = 1; i <= n; i++) {
if (!vis[a[i]]) p = a[i];
}
if (!p) {
cout << 2 << '\n';
return;
}
for (int i = 1; i <= n; i++) {
if (a[i] == p) continue;
if (vis[a[i]] == 0) {
cout << -1 << '\n';
return;
}
if (a[i] & 1) {
if (a[i] - vis[a[i]] < 2 * p) {
cout << -1 << '\n';
return;
}
} else {
if (a[i] < 2 * p) {
cout << -1 << '\n';
return;
}
}
}
cout << p << '\n';
return;
}
int main() {
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
init(400000);
cin >> T;
while (T--) {
solve();
}
}
[problem:476175F]
Author: sszcdjr
If there are both consecutive $$$\texttt{R}$$$-s and $$$\texttt{B}$$$-s, does the condition hold for all $$$(i,j)$$$? Why?
Suppose that there are only consecutive $$$\texttt{R}$$$-s, check the parity of the number of $$$\texttt{R}$$$-s in each consecutive segment of $$$\texttt{R}$$$-s.
If for each consecutive segment of $$$\texttt{R}$$$-s, the parity of the number of $$$\texttt{R}$$$-s is odd, does the condition hold for all $$$(i,j)$$$? Why?
If for at least two of the consecutive segments of $$$\texttt{R}$$$-s, the parity of the number of $$$\texttt{R}$$$-s is even, does the condition hold for all $$$(i,j)$$$? Why?
Is this the necessary and sufficient condition? Why?
Don't forget some trivial cases like $$$\texttt{RRR...RB}$$$ and $$$\texttt{RRR...R}$$$.
For each $$$k>n$$$ or $$$k\leq0$$$, let $$$c_k$$$ be $$$c_{k\bmod n}$$$.
Lemma 1: If there are both consecutive $$$\texttt{R}$$$-s and $$$\texttt{B}$$$-s, the answer is NO.
Proof 1: Suppose that $$$c_{i-1}=c_i=\texttt{R}$$$ and $$$c_{j-1}=c_j=\texttt{B}$$$, it's obvious that there doesn't exist a palindrome route between $$$i$$$ and $$$j$$$.
Imagining there are two persons on vertex $$$i$$$ and $$$j$$$. They want to meet each other (which is, they are on the same vertex or adjacent vertex) and they can only travel through an edge of the same color.
Lemma 2: Suppose that there are only consecutive $$$\texttt{R}$$$-s, if for each consecutive segment of $$$\texttt{R}$$$-s, the parity of the number of $$$\texttt{R}$$$-s is odd, the answer is NO.
Proof 2: Suppose that $$$c_i=c_j=\texttt{B}$$$, $$$i\not\equiv j(\bmod\ n)$$$ and $$$c_{i+1}=c_{i+2}=\dots=c_{j-1}=\texttt{R}$$$. The two persons on $$$i$$$ and $$$j$$$ have to "cross" $$$\texttt{B}$$$ at the same time. As for each consecutive segment of $$$\texttt{R}$$$-s, the parity of the number of $$$\texttt{R}$$$-s is odd, they can only get to the same side of there current consecutive segment of $$$\texttt{R}$$$-s. After "crossing" $$$\texttt{B}$$$, they will still be on different consecutive segment of $$$\texttt{R}$$$-s seperated by exactly one $$$\texttt{B}$$$ and can only get to the same side. Thus, they will never meet.
Lemma 3: Suppose that there are only consecutive $$$\texttt{R}$$$-s, if for at least two of the consecutive segments of $$$\texttt{R}$$$-s, the parity of the number of $$$\texttt{R}$$$-s is even, the answer is NO.
Proof 3: Suppose that $$$c_i=c_j=\texttt{B}$$$, $$$i\not\equiv j(\bmod\ n)$$$ and vertex $$$i$$$ and $$$j$$$ are both in a consecutive segment of $$$\texttt{R}$$$-s with even number of $$$\texttt{R}$$$-s. Let the starting point of two persons be $$$i$$$ and $$$j-1$$$ and they won't be able to "cross" and $$$\texttt{B}$$$. Thus, they will never meet.
The only case left is there are exactly one consecutive segment of $$$\texttt{R}$$$-s with even number of $$$\texttt{R}$$$-s.
Lemma 4: Suppose that there are only consecutive $$$\texttt{R}$$$-s, if for exactly one of the consecutive segments of $$$\texttt{R}$$$-s, the parity of the number of $$$\texttt{R}$$$-s is even, the answer is YES.
Proof 4: Let the starting point of the two persons be $$$i,j$$$. Consider the following cases:
Case 1: If vertex $$$i$$$ and $$$j$$$ are in the same consecutive segment of $$$\texttt{R}$$$-s, the two persons can meet each other by travelling through the $$$\texttt{R}$$$-s between them.
Case 2: If vertex $$$i$$$ and $$$j$$$ are in the different consecutive segment of $$$\texttt{R}$$$-s and there are odd numbers of $$$\texttt{R}$$$-s in both segments, the two person may cross $$$\texttt{B}$$$-s in the way talked about in Proof 2. However, when one of them reached a consecutive segment with even number of $$$\texttt{R}$$$-s, the only thing they can do is let the one in an even segment cross the whole segment and "cross" the next $$$\texttt{B}$$$ in the front, while let the other one travelling back and forth and "cross" the $$$\texttt{B}$$$ he just "crossed". Thus, unlike the situation in Proof 2, we successfully changed the side they can both get to, and thus they will be able to meet each other as they are travelling toward each other and there are only odd segments between them.
Case 3: If vertex $$$i$$$ and $$$j$$$ are in the different consecutive segment of $$$\texttt{R}$$$-s and there are odd number of $$$\texttt{R}$$$-s in exactly one of the segments, we can let both of them be in one side of there segments and change the situation to the one we've discussed about in Case 2 (when one of them reached a consecutive segment with even number of $$$\texttt{R}$$$-s).
As a result, the answer is YES if:
- At least $$$n-1$$$ of $$$c_1,c_2,\dots,c_n$$$ are the same (Hint 6), or
- Suppose that there are only consecutive $$$\texttt{R}$$$-s, there's exactly one of the consecutive segments of $$$\texttt{R}$$$-s such that the parity of the number of $$$\texttt{R}$$$-s is even.
And we can judge them in $$$O(n)$$$ time complexity.
#include <bits/stdc++.h>
using namespace std;
void solve(){
int n; cin>>n;
string s; cin>>s;
int visr=0,visb=0,ok=0;
for(int i=0;i<n;i++){
if(s[i]==s[(i+1)%n]){
if(s[i]=='R') visr=1;
else visb=1;
ok++;
}
}
if(visr&visb){
cout<<"NO\n";
return ;
}
if(ok==n){
cout<<"YES\n";
return ;
}
if(visb) for(int i=0;i<n;i++) s[i]='R'+'B'-s[i];
int st=0;
for(int i=0;i<n;i++) if(s[i]=='B') st=(i+1)%n;
vector<int> vc;
int ntot=0,cnt=0;
for(int i=0,j=st;i<n;i++,j=(j+1)%n){
if(s[j]=='B') vc.push_back(ntot),cnt+=(ntot&1)^1,ntot=0;
else ntot++;
}
if(vc.size()==1||cnt==1){
cout<<"YES\n";
return ;
}
cout<<"NO\n";
return ;
}
signed main(){
int t; cin>>t;
while(t--) solve();
return 0;
}
Count the number of strings length $$$n$$$ satisfying the condition.
Solve the problem for $$$c_i\in{\texttt{A,B,\dots,Z}}$$$, and solve the counting version.
[problem:476175G]
Author: _istil, Error_Yuan
This problem has two approaches. The first one is the authors' solution, and the second one was found during testing.
Coming soon.
Coming soon.
[problem:476175H]
Author: sszcdjr
It's hard to calculate the expected number. Try to change it to the probability.
Consider a $$$\mathcal{O}(3^n)$$$ dp first.
Use inclusion and exclusion.
Write out the transformation. Try to optimize it.
Let $$$dp_S$$$ be the probability such that exactly the points in $$$S$$$ has the message.
The answer is $$$\sum dp_S\cdot tr_S$$$, where $$$tr_S$$$ is the expected number of days before at least one vertex out of $$$S$$$ to have the message (counting from the day that exactly the points in $$$S$$$ has the message).
For transformation, enumerate $$$S,T$$$ such that $$$S\cap T=\varnothing$$$. Transfer $$$dp_S$$$ to $$$dp_{S\cup T}$$$. It's easy to precalculate the coefficient, and the time complexity differs from $$$\mathcal{O}(3^n)$$$, $$$\mathcal{O}(n\cdot 3^n)$$$ to $$$\mathcal{O}(n^2\cdot 3^n)$$$, according to the implementation.
The transformation is hard to optimize. Enumerate $$$T$$$ and calculate the probability such that vertices in $$$S$$$ is only connected with vertices in $$$T$$$, which means that the real status $$$R$$$ satisfies $$$S\subseteq R\subseteq (S\cup T)$$$. Use inclusion and exclusion to calculate the real probability.
List out the coefficient:
(Note that $$$w_e$$$ denotes the probability of the appearance of the edge $$$e$$$)
We can express it as $$$\mathrm{Const}\cdot f_{S\cup T}\cdot g_S\cdot h_T$$$. Use a subset convolution to optimize it. The total time complexity is $$$\mathcal{O}(2^n\cdot n^2)$$$.
It's easy to see that all $$$dp_S\neq0$$$ satisfies $$$1\in S$$$, so the time complexity can be $$$\mathcal{O}(2^{n-1}\cdot n^2)$$$ if well implemented.
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N=(1<<21),mod=998244353;
const int Lim=8e18;
inline void add(signed &i,int j){
i+=j;
if(i>=mod) i-=mod;
}
int qp(int a,int b){
int ans=1;
while(b){
if(b&1) (ans*=a)%=mod;
(a*=a)%=mod;
b>>=1;
}
return ans;
}
int dp[N],f[N],g[N],h[N];
int s1[N],s2[N];
signed pre[22][N/2],t[22][N/2],pdp[N][22];
int p[N],q[N],totp,totq;
signed main(){
int n,m; cin>>n>>m;
int totprod=1;
for(int i=0;i<(1<<n);i++) s1[i]=s2[i]=1;
for(int i=1;i<=m;i++){
int u,v,p,q; cin>>u>>v>>p>>q;
int w=p*qp(q,mod-2)%mod;
(s1[(1<<(u-1))+(1<<(v-1))]*=(mod+1-w))%=mod;
(s2[(1<<(u-1))+(1<<(v-1))]*=qp(mod+1-w,mod-2))%=mod;
(totprod*=(mod+1-w))%=mod;
}
for(int j=1;j<=n;j++) for(int i=0;i<(1<<n);i++) if((i>>(j-1))&1) (s1[i]*=s1[i^(1<<(j-1))])%=mod,(s2[i]*=s2[i^(1<<(j-1))])%=mod;
for(int i=0;i<(1<<n);i++) f[i]=s2[i],g[i]=totprod*s2[((1<<n)-1)^i]%mod*qp(mod+1-totprod*s2[i]%mod*s2[((1<<n)-1)^i]%mod,mod-2)%mod,h[i]=s1[i];
for(int i=1;i<(1<<n);i++) pre[__builtin_popcount(i)][i>>1]=h[i];
dp[1]=1;
for(int j=1;j<=n;j++){
if(!((1>>(j-1))&1)) add(pdp[1|(1<<(j-1))][j],mod-(dp[1]*g[1]%mod*f[1]%mod));
}
t[0][0]=dp[1]*g[1]%mod;
for(int k=1;k<=n;k++) for(int j=1;j<n;j++) for(int i=0;i<(1<<(n-1));i++) if((i>>(j-1))&1) add(pre[k][i],pre[k][i^(1<<(j-1))]);
for(int j=1;j<n;j++) for(int i=0;i<(1<<(n-1));i++) if((i>>(j-1))&1) add(t[0][i],t[0][i^(1<<(j-1))]);
for(int k=1;k<n;k++){
totp=totq=0;
for(int i=0;i<(1<<(n-1));i++) if(__builtin_popcount(i)<=k) p[++totp]=i; else q[++totq]=i;
for(int l=1,i=p[l];l<=totp;l++,i=p[l]) for(int j=0;j<k;j++) add(t[k][i],1ll*t[j][i]*pre[k-j][i]%mod);
for(int i=0;i<(1<<(n-1));i++) t[k][i]%=mod;
for(int j=1;j<n;j++) for(int l=1,i=p[l];l<=totp;l++,i=p[l]) if((i>>(j-1))&1) add(t[k][i],mod-t[k][i^(1<<(j-1))]);
for(int i=0;i<(1<<(n-1));i++){
if(__builtin_popcount(i)==k){
add(pdp[(i<<1)|1][0],t[k][i]*f[(i<<1)|1]%mod);
int pre=0;
for(int j=1;j<=n;j++){
(pre+=pdp[(i<<1)|1][j-1])%=mod;
if(!((((i<<1)|1)>>(j-1))&1)) add(pdp[(i<<1)|1|(1<<(j-1))][j],mod-pre);
}
(pre+=pdp[(i<<1)|1][n])%=mod;
dp[(i<<1)|1]=pre;
for(int j=1;j<=n;j++){
if(!((((i<<1)|1)>>(j-1))&1)) add(pdp[(i<<1)|1|(1<<(j-1))][j],mod-(dp[(i<<1)|1]*g[(i<<1)|1]%mod*f[(i<<1)|1]%mod));
}
t[k][i]=pre*g[(i<<1)|1]%mod;
}
else t[k][i]=0;
}
for(int j=1;j<n;j++) for(int l=1,i=q[l];l<=totq;l++,i=q[l]) if((i>>(j-1))&1) add(t[k][i],t[k][i^(1<<(j-1))]);
}
int ans=0;
for(int i=1;i<(1<<n)-1;i+=2) (ans+=dp[i]*qp(mod+1-totprod*s2[i]%mod*s2[((1<<n)-1)^i]%mod,mod-2)%mod)%=mod;
cout<<ans;
return 0;
}
[problem:476175I]
Author: Error_Yuan
The intended solution has nothing to do with dynamic programming.
This is the key observation to the problem. Suppose we have an array $$$b$$$ and a function $$$f(x)=\sum (b_i-x)^2$$$, then the minimum value of $$$f(x)$$$ is the variance of $$$b$$$.
Using the observation mentioned in Hint 2, we can reduce the problem to minimizing $$$\sum(a_i-x)^2$$$ for a given $$$x$$$. There are only $$$\mathcal{O}(n\cdot m)$$$ possible $$$x$$$-s.
The rest of the problem is way easy. Try flows, or just find a greedy algorithm!
If you are trying flows: the quadratic function is always convex.
Key Observation. Suppose we have an array $$$b$$$ and a function $$$f(x)=\sum (b_i-x)^2$$$, then the minimum value of $$$f(x)$$$ is the variance of $$$b$$$.
Proof. This is a quadratic function of $$$x$$$, and the its symmetry axis is $$$x=\frac{1}{n}\sum b_i$$$. So the minimum value is $$$f\left(\frac{1}{n}\sum b_i\right)$$$. That is exactly the definition of variance.
Thus, we can enumerate all possible $$$x$$$-s, and find the minimum $$$\sum (a_i-x)^2$$$ after the operations, then take the minimum accross them. That will give the correct answer to the original problem. Note that there are only $$$\mathcal{O}(n\cdot m)$$$ possible $$$x$$$-s.
More formally, let $$$k_{x,c}$$$ be the minimum value of $$$\sum (a_i-x)^2$$$ after exactly $$$c$$$ operations. Then $$$\mathrm{ans}_i=\displaystyle\min_{\text{any possible }x} k_{x,i}$$$.
So we only need to solve the following (reduced) problem:
- Given an (maybe non-integer) number $$$x$$$. For each $$$1\le i\le m$$$, find the minimum value of $$$\sum (a_i-x)^2$$$ after exactly $$$i$$$ operations.
To solve this, we can use the MCMF model:
- Set a source node $$$s$$$ and a target node $$$t$$$.
- For each $$$1\le i\le n$$$, add an edge from $$$s$$$ to $$$i$$$ with cost $$$0$$$.
- For each $$$1\le i\le n$$$, add an edge from $$$i$$$ to $$$t$$$ with cost $$$0$$$.
- For each $$$1\le i< n$$$, add an edge from $$$i$$$ to $$$i+1$$$ with cost being a function $$$\mathrm{cost}(f)=(a_i+f-x)^2-(a_i-x)^2$$$, where $$$f$$$ is the flow on this edge.
- Note that the $$$\mathrm{cost}$$$ function is convex, so this model is correct, as you can split an edge into some edges with cost of $$$\mathrm{cost}(1)$$$, $$$\mathrm{cost}(2)-\mathrm{cost}(1)$$$, $$$\mathrm{cost}(3)-\mathrm{cost}(2)$$$, and so on.
Take a look at the model again. We don't need to run MCMF actually. We can see that it is just a process of regret greedy. So you only need to find the LIS (Largest Interval Sum :) ) for each operation.
Thus, we solved the reduced problem in $$$\mathcal{O(n\cdot m)}$$$.
Overall time complexity: $$$\mathcal{O}((n\cdot m)^2)$$$ per test case.
Reminder: don't forget to use __int128 if you didn't handle the numbers carefully!
#include <bits/stdc++.h>
#define all(s) s.begin(), s.end()
using namespace std;
using ll = long long;
using ull = unsigned long long;
const int _N = 1e5 + 5;
int T;
void solve() {
ll n, m, k; cin >> n >> m >> k;
vector<ll> a(n + 1);
for (int i = 1; i <= n; i++) cin >> a[i];
vector<ll> kans(m + 1, LLONG_MAX);
vector<__int128> f(n + 1), g(n + 1), v(n + 1);
vector<int> vis(n + 1), L(n + 1), L2(n + 1);
ll sum = 0;
for (int i = 1; i <= n; i++) sum += a[i];
__int128 pans = 0;
for (int i = 1; i <= n; i++) pans += n * a[i] * a[i];
auto work = [&](ll s) {
__int128 ans = pans;
ans += s * s - 2ll * sum * s;
f.assign(n + 1, LLONG_MAX);
g.assign(n + 1, LLONG_MAX);
for (int i = 1; i <= n; i++) {
v[i] = n * (2 * a[i] * k + k * k) - 2ll * s * k;
vis[i] = 0;
}
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
L[j] = L2[j] = j;
if (f[j - 1] < 0) f[j] = f[j - 1] + v[j], L[j] = L[j - 1];
else f[j] = v[j];
if (!vis[j]) {
g[j] = LLONG_MAX;
continue;
}
if (g[j - 1] < 0) g[j] = g[j - 1] + 2ll * n * k * k - v[j], L2[j] = L2[j - 1];
else g[j] = 2ll * n * k * k - v[j];
}
__int128 min_sum = LLONG_MAX;
int l = 1, r = n, type = 0;
for (int j = 1; j <= n; j++) {
if (f[j] < min_sum) {
min_sum = f[j], r = j, l = L[j];
}
}
for (int j = 1; j <= n; j++) {
if (g[j] < min_sum) {
min_sum = g[j], r = j, l = L2[j];
type = 1;
}
}
ans += min_sum;
if (type == 0) {
for (int j = l; j <= r; j++) vis[j]++, v[j] += 2 * n * k * k;
} else {
for (int j = l; j <= r; j++) vis[j]--, v[j] -= 2 * n * k * k;
}
kans[i] = min((__int128)kans[i], ans);
}
};
for (ll x = sum; x <= sum + n * m * k; x += k) {
work(x);
}
for (int i = 1; i <= m; i++) cout << kans[i] << " \n"[i == m];
return;
}
int main() {
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
cin >> T;
while (T--) {
solve();
}
}





