| A | B | C | D | E | F | G | H | I | |
|---|---|---|---|---|---|---|---|---|---|
| Error_Yuan | 800 | 1200 | 1600 | 2100 | 2300 | 2600 | 3000 | 3400 | 3500 |
| sszcdjr | 800 | 1100 | 1600 | 2000 | 2300 | 2600 | 2900 | 3300 | 3500 |
| _istil | 800 | 1000 | 1400 | 2200 | 2300 | 2600 | 3000 | 3500 | 3500 |
[problem:476175A]
Author: Otomachi_Una
Greedy from small to large.
We can delete the numbers from small to large. Thus, previously removed numbers will not affect future choices (if $$$x<y$$$, then $$$x$$$ cannot be a multiple of $$$y$$$). So an integer $$$x$$$ ($$$l\le x\le r$$$) can be removed if and only if $$$k\cdot x\le r$$$, that is, $$$x\le \left\lfloor\frac{r}{k}\right\rfloor$$$. The answer is $$$\max\left(\left\lfloor\frac{r}{k}\right\rfloor-l+1,0\right)$$$.
Time complexity: $$$\mathcal{O}(1)$$$ per test case.
#include <bits/stdc++.h>
#define all(s) s.begin(), s.end()
using namespace std;
using ll = long long;
using ull = unsigned long long;
const int _N = 1e5 + 5;
int T;
void solve() {
int l, r, k; cin >> l >> r >> k;
cout << max(r / k - l + 1, 0) << endl;
return;
}
int main() {
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
cin >> T;
while (T--) {
solve();
}
}
for _ in range(int(input())):
l, r, k = map(int, input().split())
print(max(r // k - l + 1, 0))
[problem:476175B]
Author: _istil
($$$\texttt{01}$$$ or $$$\texttt{10}$$$ exists) $$$\Longleftrightarrow$$$ (both $$$\texttt{0}$$$ and $$$\texttt{1}$$$ exist).
Each time we do an operation, if $$$s$$$ consists only of $$$\texttt{0}$$$ or $$$\texttt{1}$$$, we surely cannot find any valid indices. Otherwise, we can always perform the operation successfully. In the $$$i$$$-th operation, if $$$t_i=\texttt{0}$$$, we actually decrease the number of $$$\texttt{1}$$$-s by $$$1$$$, and vice versa. Thus, we only need to maintain the number of $$$\texttt{0}$$$-s and $$$\texttt{1}$$$-s in $$$s$$$. If any of them falls to $$$0$$$ before the last operation, the answer is NO, otherwise, the answer is YES.
Time complexity: $$$\mathcal{O}(n)$$$ per test case.
#include <bits/stdc++.h>
#define all(s) s.begin(), s.end()
using namespace std;
using ll = long long;
const int _N = 1e5 + 5;
void solve() {
int n; cin >> n;
string s, t; cin >> s >> t;
int cnt0 = count(all(s), '0'), cnt1 = n - cnt0;
for (int i = 0; i < n - 1; i++) {
if (cnt0 == 0 || cnt1 == 0) {
cout << "NO" << '\n';
return;
}
if (t[i] == '1') cnt0--;
else cnt1--;
}
cout << "YES" << '\n';
}
int main() {
int T; cin >> T;
while (T--) {
solve();
}
}
for _ in range(int(input())):
n = int(input())
s = input()
one = s.count("1")
zero = s.count("0")
ans = "YES"
for ti in input():
if one == 0 or zero == 0:
ans = "NO"
break
one -= 1
zero -= 1
if ti == "1":
one += 1
else:
zero += 1
print(ans)
[problem:476175C]
Author: Error_Yuan
Binary search.
Do something backward.
First, do binary search on the answer. Suppose we're checking whether the answer can be $$$\ge k$$$ now.
Let $$$f_i$$$ be the current rating after participating in the $$$1$$$-st to the $$$i$$$-th contest (without skipping).
Let $$$g_i$$$ be the minimum rating before the $$$i$$$-th contest to make sure that the final rating is $$$\ge k$$$ (without skipping).
$$$f_i$$$-s can be calculated easily by simulating the process in the statement. For $$$g_i$$$-s, it can be shown that
where $$$g_{n+1}=k$$$.
Then, we should check if there exists an interval $$$[l,r]$$$ ($$$1\le l\le r\le n$$$), such that $$$f_{l-1}\ge g_{r+1}$$$. If so, we can choose to skip $$$[l,r]$$$ and get a rating of $$$\ge k$$$. Otherwise, it is impossible to make the rating $$$\ge k$$$.
We can enumerate on $$$r$$$ and use a prefix max to check whether valid $$$l$$$ exists.
Time complexity: $$$\mathcal{O}(n\log n)$$$.
Consider DP.
There are only three possible states for each contest: before, in, or after the skipped interval.
Consider $$$dp_{i,0/1/2}=$$$ the maximum rating after the $$$i$$$-th contest, where the $$$i$$$-th contest is before/in/after the skipped interval.
Let $$$f(a,x)=$$$ the result rating when current rating is $$$a$$$ and the performance rating is $$$x$$$, then
And the final answer is $$$\max(dp_{n,1}, dp_{n,2})$$$.
Time complexity: $$$\mathcal{O}(n)$$$.
#include <bits/stdc++.h>
#define all(s) s.begin(), s.end()
using namespace std;
using ll = long long;
using ull = unsigned long long;
const int _N = 1e5 + 5;
int T;
void solve() {
int n; cin >> n;
vector<int> a(n + 1);
for (int i = 1; i <= n; i++) cin >> a[i];
vector<int> pre(n + 1);
int curf = 0;
for (int i = 1; i <= n; i++) {
if (curf < a[i]) curf++;
else if (curf > a[i]) curf--;
pre[i] = max(pre[i - 1], curf);
}
auto check = [&](int k) {
int curg = k;
for (int i = n; i >= 1; i--) {
if (pre[i - 1] >= curg) return true;
if (a[i] < curg) curg++;
else curg--;
}
return false;
};
int L = 0, R = n + 1;
while (L < R) {
int mid = (L + R + 1) >> 1;
if (check(mid)) L = mid;
else R = mid - 1;
}
cout << L << '\n';
return;
}
int main() {
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
cin >> T;
while (T--) {
solve();
}
}
for _ in range(int(input())):
n = int(input())
def f(a, x):
return a + (a < x) - (a > x)
dp = [0, -n, -n]
for x in map(int, input().split()):
dp[2] = max(f(dp[1], x), f(dp[2], x))
dp[1] = max(dp[1], dp[0])
dp[0] = f(dp[0], x)
print(max(dp[1], dp[2]))
[problem:476175D]
Author: Error_Yuan
There are many different approaches to this problem. Only the easiest one (at least I think so) is shared here.
Try to make the graph into a forest first.
Let $$$d_i$$$ be the degree of vertex $$$i$$$.
($$$d_i\le 1$$$ for every $$$i$$$) $$$\Longrightarrow$$$ (The graph is a forest).
Let $$$d_i$$$ be the degree of vertex $$$i$$$.
First, we keep doing the following until it is impossible:
- Choose a vertex $$$u$$$ with $$$d_u\ge 2$$$, then find any two vertices $$$v,w$$$ adjacent to $$$u$$$. Perform the operation on $$$(u,v,w)$$$.
Since each operation decreases the number of edges by at least $$$1$$$, at most $$$m$$$ operations will be performed. After these operations, $$$d_i\le 1$$$ holds for every $$$i$$$. Thus, the resulting graph consists only of components with size $$$\le 2$$$.
If there are no edges, the graph is already cool, and we don't need to do any more operations.
Otherwise, let's pick an arbitrary edge $$$(u,v)$$$ as the base of the final tree, and then merge everything else to it.
For a component with size $$$=1$$$ (i.e. it is a single vertex $$$w$$$), perform the operation on $$$(u, v, w)$$$, and set $$$(u, v) \gets (u, w)$$$.
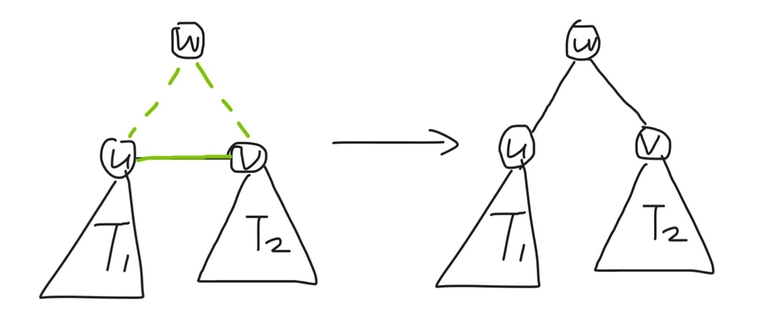
For a component with size $$$=2$$$ (i.e. it is an edge connecting $$$a$$$ and $$$b$$$), perform the operation on $$$(u, a, b)$$$.
It is clear that the graph is transformed into a tree now.
[problem:476175E]
Author: Error_Yuan, _istil
[problem:476175F]
Author: sszcdjr
[problem:476175G]
Author: _istil, Error_Yuan
[problem:476175H]
Author: sszcdjr
[problem:476175I]
Author: Error_Yuan





