Introduction
A classical problem reads:
Count the paths from $$$(0,0)$$$ to $$$(m,n)(n>m>0)$$$ that doesn't go through $$$y=x$$$ (the path can touch the line). One can only move up or right by $$$1$$$ in one move.
The problem can also be described as:
Count binary strings that consist of $$$m$$$ zeros and $$$n$$$ ones $$$(n\ge m)$$$, such that in every prefix of the string, the number of zeros doesn't exceed the number of ones.
Consider how to count paths from $$$(0,0)$$$ to $$$(m,n)$$$ without the intersection restriction. To get to $$$(m,n)$$$, we must move up $$$n$$$ times and move right $$$m$$$ times. In other words, we need to permute $$$n$$$ right and $$$m$$$ up, whose quantity is
To count the paths that doesn't intersect, we can try to count the paths that go through $$$y=x$$$, and this is when the reflection principle is utilized. The principle says:
Given point $$$A,B$$$ at the same side of line $$$l$$$, the number of paths from $$$A$$$ to $$$B$$$ that intersect with $$$l$$$ is equal to that of paths from $$$A^\prime$$$ to $$$B$$$, where $$$A^\prime$$$ is the reflection point through $$$l$$$.
To show why it is correct, we should first note that a path from $$$A^\prime$$$ to $$$B$$$ must intersect with $$$y=x$$$. Say at point $$$P$$$ the path first intersect with $$$y=x$$$, we can reflect the path from $$$A^\prime$$$ to $$$P$$$ through $$$l$$$ and get a path from $$$A$$$ to $$$B$$$, and vice versa. This indicates that the intersecting paths from $$$A$$$ to $$$B$$$ and the paths from $$$A^\prime$$$ and $$$B$$$ are one-to-one corresponded, and the quantity of the two are the same.
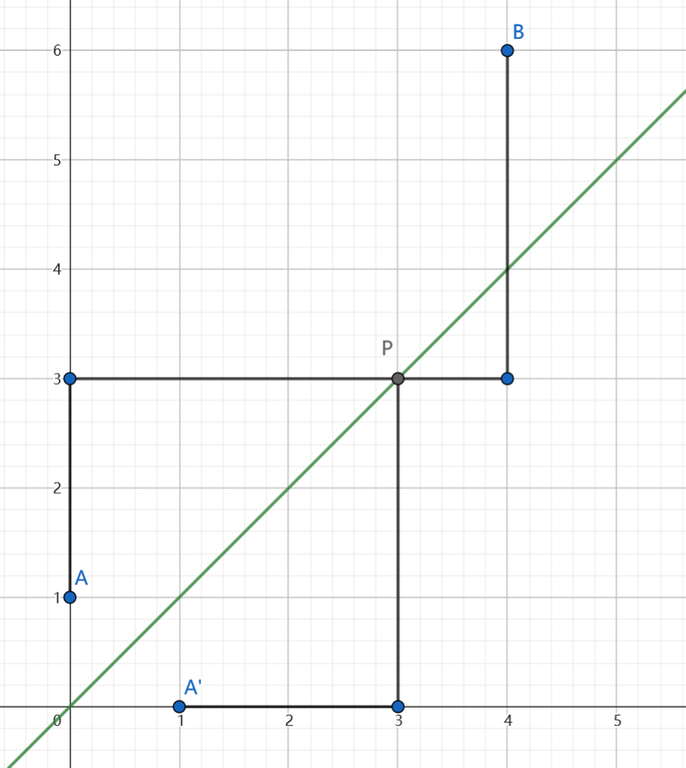
Back to our problem. Going through $$$y=x$$$ is the same as intersecting with $$$y=x-1$$$ in this case, so $$$(0,0)$$$ can reflected to $$$(1,-1)$$$, and the number of intersecting path is $$$\binom{m+n}{m-1}$$$. Therefore, the answer to the problem is
In particular, when $$$n=m$$$, the formula becomes
which is the Catalan number.
Examples
105390D - String From Another World






