Greetings Everyone,
I was doing the maximum enclosing circle problem, This is the subproblem of that.
Given two ends points of a common chord of two circles of equal radius say R find out the coordinates of two centers of the circles (without much precision loss preferably)
The condition can be pictorially represented like.

A possible solution might be to find the coordinates of mid point of A and B that is M which is 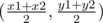
Since the slope of line joining A and B is 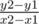 and since the line joining the centers would be perpendicular to the slope of line joining C1 and C2 would be
and since the line joining the centers would be perpendicular to the slope of line joining C1 and C2 would be 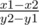 .
.
The distance between the points M and C1 or C2 can be found using pythagoras theorem i.e. 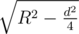 where
where 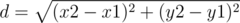
Now since we know the slope of the line and a point on it and distance between the points we can now find the coordinates of centers, but It's highly insensitive to precision.
Any other method, resource , links etc would be deeply appreciated.
Thanks in advance.






