Let n is a positive integer.

n = p₁^e₁p₂^e₂...p_k^e_k is the complete prime factorization of n.

Let me define a function f(n)

f(n) = p₁^c₁p₂^c₂...p_k^c_k where c_k = e_k if e_k is divisible by p_k, otherwise c_k = e_k - 1

Example:

72 = 2³³², so f(72) = 2^3 - 13^2 - 1 = 2²3¹ = 12

144 = 2⁴³², so f(144) = 2⁴3^2 - 1 = 2⁴3¹ = 48, as 4 is divisible by 2, exponent of 2 remains same.

Now let

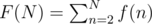
Example: F(10) = 1 + 1 + 4 + 1 + 1 + 1 + 4 + 3 + 1 = 17

Now I want to evaluate F(N) for a fairly large value of N, say 10¹⁴. Can I do it without factorizing each number?

It is more difficult than the previous one.