One can notice that the maximum cost of sending a letter from i'th city is equal to maximum of distances from i'th city to first city and from i'th city to last (max(abs(xi - x0), abs(xi - xn - 1)). On the other hand, the minimum cost of sending a letter will be the minimum of distances between neighboring cities (i - 1'th and i + 1'th cities), more formally, min(abs(xi - xi - 1), abs(xi - xi + 1). For each city, except the first and the last this formula is correct, but for them formulas are (abs(xi - xi + 1)) and (abs(xi - xi - 1)) respectively.
567B - Berland National Library
To answer the queries correct, we need to know if the person is still in the library. For that purpose we will use in array of type bool. Also we will store two variables for the answer and ''current state'' (it will store the current number of people in the library). Let's call them ans and state respectively.
Thus, if we are given query + ai then we should increase state by one, mark that this person entered the library (in[ai] = true) and try to update the answer (ans = max(ans, state)).
Otherwise we are given - ai query. If the person who leaves the library, was in there, we should just decrease state by one. Otherwise, if this person was not in the library (in[ai] == false) and leaves now, he entered the library before we started counting. It means we should increase the answer by one anyway. Also one should not forget that it is needed to mark that the person has left the library (in[ai] = false).
Let's solve this problem for fixed middle element of progression. This means that if we fix element ai then the progression must consist of ai / k and ai·k elements. It could not be possible, for example, if ai is not divisible by k (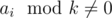 ).
).
For fixed middle element one could find the number of sequences by counting how many ai / k elements are placed left from fixed element and how many ai·k are placed right from it, and then multiplying this numbers. To do this, one could use two associative arrays Al and Ar, where for each key x will be stored count of occurences of x placed left (or right respectively) from current element. This could be done with map structure.
Sum of values calculated as described above will give the answer to the problem.
567D - One-Dimensional Battle Ships
Editorial to this task will be posted later.
Editorial to this task will be posted later.
Editorial to this task will be posted later.







