569A - Music

Пусть перед очередным запуском прогружено S секунд песни, найдем, сколько будет прогружено перед следующим запуском. 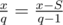. Отсюда x = qS.

Тогда решение: будем умножать S на q пока S < T. Количество таких умножений — это ответ.

Сложность —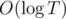

569B - Inventory

Подойдём к задаче с другой стороны: а сколько максимально можно оставить номеров, чтобы получилась перестановка? Очевидно, что эти номера должны быть от 1 до n, причем среди них не должно быть повторяющихся. И понятно, что это условие необходимое и достаточное.

Такую задачу можно решать жадным алгоритмом. Если мы встретили число, которого ещё не было, при этом оно от 1 до n, то мы его оставим. Для реализации можно завести массив used, в котором отмечать уже использованные числа.

Затем нужно ещё раз пройти по массиву и распределить неиспользованные числа.

Сложность — O(n).

568A - Primes or Palindromes?

Известно, что количество простых чисел, не превосходящих n, — число порядка .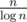

Если мы зафиксируем длину числа k, то количество палиндромных чисел такой длины будет порядка 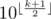. Это .

Таким образом, количество простых чисел асимптотически больше количества палиндромных чисел, а значит для любой константы A найдётся ответ. И для такого ответа 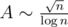. В нашем случае n будут не больше 10⁷.

Поэтому мы можем для всех чисел до 10⁷ проверить, являются ли они простыми (с помощью решета Эратосфена), а также являются ли они палиндромными (с помощью наивного алгоритма, или же можно динамикой считать зеркальное отображение числа). Затем мы посчитаем префиксные суммы, а потом линейным поиском найдём ответ.

При A ≤ 42 ответ не превышает 2·10⁶.

Сложность — .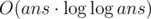

568B - Symmetric and Transitive

Давайте сначала разберёмся, в чем же конкретно неправ Вовочка. В доказательстве хорошо всё, кроме того, что мы сразу взяли a, b такие, что 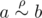. Если такие есть, то действительно 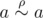. А если их нет? Если для a нет такого b, что 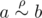, то, очевидно, не 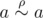(иначе мы бы взяли b = a).

Отсюда понятно, что наше бинарное отношение — это какое-то отношение эквивалентности, к которому присоединили такие элементы a, что для всех них не существует таких b, что .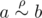

Тогда решение можно разбить на две части:

1. Посчитать количество отношений эквивалентности на множествах размеров 0, 1, ..., n - 1

2. Посчитать, сколькими способами туда можно добавить недостающие "пустые" элементы.

Отношение эквивалентности можно задать разбиением на классы эквивалентности.

Тогда первую часть задачи можно решить динамическим программированием: dp[elems][classes] — кол-во способов разбить elems первых элементов на classes классов эквивалентности. Переход — каждый элемент мы можем либо отнести в один из уже существующих классов, тогда их количество не изменится, либо же создать новый класс, тогда их количество увеличится на 1.

Вторая часть задачи. Зафиксируем m — размер множества, над которым мы посчитали количество отношений эквивалентности. Тогда нам нужно добавить к нему ещё n - m "пустых" элементов. Позиции для них можно выбрать C[n][n - m] способами, где C[n][k] — биномиальные коэффициенты. Их можно заранее посчитать треугольником Паскаля.

Тогда ответ — .

Сложность — O(n²)

568C - New Language

Пусть мы зафиксировали буквы на каких-то позициях, как проверить, что на остальные позиции можно расставить буквы так, чтобы получилось слово из языка? Ответ — 2-SAT. Действительно, для каждой позиции есть два взаимоисключающих варианта (гласная и согласная), а правила языка — это импликации. Таким образом, такую проверку мы можем сделать за O(n + m).

Будем уменьшать длину префикса, который мы оставляем таким же, как у слова s. Тогда следующая буква должна быть строго больше, чем в s, а весь дальнейший суффикс может быть любым. Переберём эту букву и проверим с помощью 2-SAT, есть ли решения. Как только мы обнаружили, что решения есть, мы нашли правильный префикс лексиграфически минимального ответа. Затем будем обратно наращивать префикс, какая-то из букв точно подойдёт. Мы получили решение за O(nmΣ ). Σ из решения можно убрать, заметив, что каждый раз нам нужно проверять только минимальные подходящие гласную и согласную буквы.

Также нужно не забыть случай, когда все буквы в языке одной гласности.

Сложность — O(nm)

568D - Sign Posts

Предположим, что решение есть. Если n ≤ k, то мы можем на каждую дорогу поставить по столбу. Иначе рассмотрим любые k + 1 дорогу. По принципу Дирихле среди них найдутся две, для которых будет общий указатель. Переберём эту пару дорог, поставим столб на их пересечение, уберем дороги, которые тоже проходят через эту точку. Мы свели задачу к меньшему числу столбов. Таким рекурсивным перебором мы решим задачу (если решение существует).

Решение это работает за 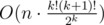. Если написать аккуратно, это может зайти.

Но это решение можно ускорить. Заметим, что если у нас есть точка, через которую проходит хотя бы k + 1 дорога, то мы обязаны поставить столб в эту точку. При достаточно больших n (у меня в решении отсечка n > 30k²) такая точка точно есть (если решение существует), причём её можно искать вероятностным алгоритмом. При условии, что решение существует, вероятность, что две произвольные дороги пересекаются в такой точке не меньше 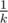, поэтому если попробовать 100 раз, то с вероятностью 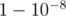такая точка найдется, и мы сможем уменьшить k.

Все проверки можно делать в целых числах.

Сложность — .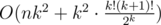

568E - Longest Increasing Subsequence

Будем поддерживать массив c: c[len] — минимальное число, на которое может заканчиваться возрастающая подпоследовательность длины len (Одно из двух стандартных решений задачи о наибольшей возрастающей подпоследовательности). Элементы этого массива возрастают и добавление очередного элемента v к обработанной части последовательности сводится к нахождению такого i, что c[i] ≤ v и c[i + 1] ≥ v. При обработке пропуска нам нужно попробовать вставить все числа из множества b. Предварительно их отсортировав и двигаясь двумя указателями вдоль массивов b и c мы можем проделать нужные обновления за O(n + m).

Авторами подразумевалось использование O(n) памяти для восстановления ответа. Этого можно добиться следующим образом: 1. Параллельно с массивом c будем хранить массив c_index[len] — индекс элемента, на который заканчивается оптимальная НВП длины len. Если она заканчивается в пропуске — будем хранить, например,  - 1. 2. Также сохраним для каждого не пропуска — длину НВП(lenLIS[pos]), заканчивающейся в этой позиции (это несложно делается в процессе вычисления массива c) и позицию(prevIndex[pos]) предыдущего элемента в этой НВП (если это пропуск, опять же  - 1).

Теперь приступим к восстановлению ответа. Пока мы не наткнулись на пропуск — можно спокойно восстанавливать НВП с конца. Сложность обнаруживается, когда несколько следующих элементов последовательности попали в пропуски. Но можно несложно определить что это за пропуски и чем их заполнить. А именно: пусть сейчас мы стоим в позиции r. Нам нужно найти такую позицию l (не пропуск), что мы сможем заполнить ровно lenLIS[r] - lenLIS[l] пропусков между l и r возрастающими числами в интервале (a[l]..a[r]). Позицию l можно итеративно перебирать от r - 1 до 0, параллельно насчитывая число пройденных пропусков. Проверку условия описанного выше можно несложно сделать с помощью пары бинпоисков.

Немного подробнее и с деталями:

1. Как узнать, что между позициями l и r можно заполнить пропуски так, чтобы не ухудшить генерируемый ответ?
   Пусть countSkip(l, r) — количество пропусков на интервале (l..r), а countBetween(x, y) — количество различных чисел из множества b, лежaщих в интервале (x..y). Тогда позиции l и r хорошие тогда и только тогда, когда lenLIS[r] - lenLIS[l] = min(countSkip(l, r), countBetween(a[l], a[r])). countSkip можно насчитывать в процессе уменьшения границы l, countBetween(x, y) = max(0, lower_bound(b, y) - upper_bound(b, x)).

2. Что делать, если НВП заканчивается или начинается в пропуске (тогда мы не знаем, откуда начать/где закончить)?
   Наиболее простым решением будет добавить  - ∞ и  + ∞ в начало и конец нашего массива соответственно. Это позволит избежать проблем с такими крайними случаями.

Сложность — 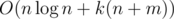времени, O(n + m) памяти