622A - Infinite Sequence

Let's decrease n by one. Now let's determine the block with the n-th number. To do that let's at first subtract 1 from n, then subtract 2, then subtract 3 and so on until we got negative n. The number of subtractions will be the number of the block and the position in the block will be the last nonnegative number we will get.

С++ solution

Complexity: .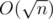

622B - The Time

In this problem we can simply increase a times the current time by one minute (after each increasing we should check the hours and the minutes for overflow).

Another solution is to use the next formulas as the answer: .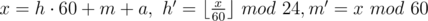

C++ solution 1

C++ solution 2

Complexity: O(a) or O(1).

622C - Not Equal on a Segment

This problem is a simplified version of the problem suggested by Mohammad Nematollahi Deemo.

This problem can be solved differently. For example you can use some data structures or sqrt-decomposition technique. But it is not required. We expected the following simple solution from the participants. Let's preprocess the following values p_i — the position of the first element to the left from the i-th element such that a_i ≠ a_pi. Now to answer to the query we should check if a_r ≠ x then we have the answer. Otherwise we should check the position p_r.

C++ solution

Complexity: O(n).

622D - Optimal Number Permutation

This problem was suggested by Aleksa Plavsic allllekssssa.

Let's build the answer with the sum equal to zero. Let n be even. Let's place odd numbers in the first half of the array: the number 1 in the positions 1 and n, the number 3 in the positions 2 and n - 1 and so on. Similarly let's place even numbers in the second half: the number 2 in the position n + 1 and 2n - 1, the number 4 in the positions n + 2 and 2n - 2 and so on. We can place the number n in the leftover positions. We can build the answer for odd n in a similar way.

Easy to see that our construction will give zero sum.

C++ solution

Complexity: O(n).

622E - Ants in Leaves

This problem was suggested by Aleksa Plavsic allllekssssa.

Easy to see that the answer is equal to the answer over all sons of the root plus one. Now let's solve the problem independently for each son v of the root. Let z be the array of the depths of all leaves in the subtree of the vertex v. Let's sort z. Statement 1: it's profitable to lift the leaves in order of their appearing in z. Statement 2: denote a_x — the time of appearing the x-th leaf in the vertex v, let's consider the leaves z_i and z_i + 1 then a_zi + 1 ≥ a_zi + 1. Statement 3: a_zi + 1 = max(d_zi + 1, a_zi + 1), where d_x is the depth of the x-th leaf in the subtree of the vertex v. The last statement gives us the solution for the problem: we should simply iterate over z from left to right and recalculate the array a by formula from the third statement. All statements can be easily proved and it's recommended to do by yourself to understand better the idea of the solution.

С++ solution

Complexity: O(nlogn).

622F - The Sum of the k-th Powers

This problem was suggested by Ivan Popovich NVAL.

Statement: the function of the sum is a polynomial of degree k + 1 over variable n. This statement can be proved by induction (to make step you should take the derivative).

Denote P_x the value of the sum for n = x. We can easily calculate the values of P_x for x from 0 to k + 1 in O(klogk) time. If n < k + 2 then we already have the answer. Otherwise let's use Lagrange polynomial to get the value of the sum for the given value n.

The Largange polynomial have the following form: 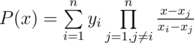. In our case x_i = i - 1 and y_i = P_xi.

To calculate P(n) in a linear time we should use that x_i + 1 - x_i = x_j + 1 - x_j for all i, j < n. It's help us because with that property we can recalculate the inner product for i + 1 from the inner product for i simply by multiplying by two values and dividing by two values. So we can calculate the sum in linear time over k.

С++ solution

Complexity: O(klog MOD) (logk appeared because we should find the inverse element in the field modulo MOD = 10⁹ + 7).