622A - Infinite Sequence
Вычтем из числа n единицу. Определим сначала номер блока в который попало n-е число. Для это сначала вычтем из числа n число 1, затем 2, затем 3 и так далее пока n не станет отрицательным. Количество вычитаний и будем номером блока, а позицией в блоке будет последнее неотрицательное число, которое мы встретим.
Сложность:  .
.
622B - The Time
В этой задаче можно было a раз прибавлять к текущему времени по одной минуте, аккуратно обрабатывая переполнения часов и минут.
А можно было просто посчитать ответ формулой: 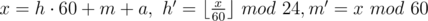 .
.
Сложность: O(a) or O(1).
622C - Not Equal on a Segment
Задача является значительно упрощённой версией задачи предложенной Mohammad Nematollahi Deemo.
Эту задачу можно было решать по разному, например, с помощью структур данных или sqrt-декомпозиции. Но это, конечно, делать не требовалось. Мы предполагали следующее простое линейное решение. Сделаем сначала предподсчет: для каждого числа номер первого не равного ему слева. Теперь, чтобы ответить на запрос нужно сначала проверить число в правой границе на равентсво числу x, если они не равны то мы уже нашли ответ. Если же они равны проверим первое число слева не равное числу в правой границе.
Сложность: O(n).
622D - Optimal Number Permutation
Задача предложена Aleksa Plavsic allllekssssa.
Давайте построим ответ в котором сумма будет равна 0. Пусть n чётно. Давайте расставим нечётные числа в первой половине массива: число 1 в позициях 1 и n, число 3 позициях 2 и n - 1 и так далее. Аналогично давайте расставим чётные числа во второй половине массива: число 2 в позициях n + 1 и 2n - 1, число 4 в позициях n + 2 и 2n - 2 и так далее. Число n мы можем поставить в оставшихся в конце свободных позициях. По аналогии ответ строится для нечётного n.
Легко видеть, что при данном построении искомая сумма равна 0.
Сложность: O(n).
622E - Ants in Leaves
Задача предложена Aleksa Plavsic allllekssssa.
Легко видеть, что ответ равен максимуму из ответов по сыновьям корня плюс один. Теперь давайте решать задачу отдельно для каждого сына v корня. Пусть z — массив глубин всех листьев в поддереве вершины v. Отсортируем z. Утверждение 1: листья выгодно поднимать в вершину v в порядке сортировки в массиве z. Утверждение 2: обозначим ax — время попадания x-го листа в вершину v и рассмотрим листья zi и zi + 1, тогда azi + 1 ≥ azi + 1. Утверждение 3: azi + 1 = max(dzi + 1, azi + 1), где dx — глубина листа x в поддереве вершины v. Последнее утверждение даём нам решение задачи: нужно просто итерироваться по массиву z слева направо и пересчитывать массив a согласно формуле из утверждения 3. Все три утверждения легко доказать и это предлагается сделать самостоятельно, чтобы лучше понять как решение работает.
Сложность: O(nlogn).
622F - The Sum of the k-th Powers
Задача предложена Иваном Поповичем NVAL.
Утверждение: функция суммы является многочленом k + 1-й степени относительно переменной n. Это утверждение можно доказать по-разному, например, можно доказать методом математической индукции (для перехода нужно взять производную от текущего многочлена).
Обозначим Px значение искомой суммы при n = x. Вычислим значения Px для всех целых значений от 0 до k + 1 (это легко сделать одним циклом за линейное время). Если n < k + 2, то мы уже нашли ответ. В противном случае давайте воспользуемся интерполяционным многочленом Лагранжа для получения искомого многочлена относительно переменной n.
Формула интерполяционного многочлена Лагранжа имеет вид: 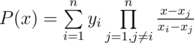 .
.
На этом разбор задачи был бы окончен, но это решение работает за квадратичное время от k, поскольку многочлен Лагранжа вычисляется за квадратичное время. Заметим, что у нас все узлы при интерполяции находятся на одинаковом расстоянии друг от друга (на расстоянии 1). Воспользуемся этим: заметим, что произведение внутри суммы для i + 1 может быть получено из произведения для i (нужно домножить текущее произведение на два числа и поделить на два числа). Таким образом, искомая сумма может быть посчитана за линейное время от k.
Сложность: O(klogk), логарифм повляется в связи с необходимостью поиска обратного элемента в поле по модулю 109 + 7.







