622A - Infinite Sequence
Let's decrease n by one. Now let's determine the block with the n-th number. To do that let's at first subtract 1 from n, then subtract 2, then subtract 3 and so on until we got negative n. The number of subtractions will be the number of the block and the position in the block will be the last nonnegative number we will get.
Complexity: 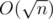 .
.
622B - The Time
In this problem we can simply increase a times the current time by one minute (after each increasing we should check the hours and the minutes for overflow).
Another solution is to use the next formulas as the answer: 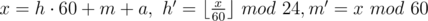 .
.
Complexity: O(a) or O(1).
622C - Not Equal on a Segment
This problem is a simplified version of the problem suggested by Mohammad Nematollahi Deemo.
This problem can be solved differently. For example you can use some data structures or sqrt-decomposition technique. But it is not required. We expected the following simple solution from the participants. Let's preprocess the following values pi — the position of the first element to the left from the i-th element such that ai ≠ api. Now to answer to the query we should check if ar ≠ x then we have the answer. Otherwise we should check the position pr.
Complexity: O(n).
622D - Optimal Number Permutation
This problem is suggested by Aleksa Plavsic allllekssssa.
Let's build the answer with the sum equal to zero. Let n be even. Let's place odd numbers in the first half of the array: the number 1 in the positions 1 and n, the number 3 in the positions 2 and n - 1 and so on. Similarly let's place even numbers in the second half: the number 2 in the position n + 1 and 2n - 1, the number 4 in the positions n + 2 and 2n - 2 and so on. We can place the number n in the leftover positions. We can build the answer for odd n in a similar way.
Easy to see that our construction will give zero sum.
Complexity: O(n).







