652A - Gabriel and Caterpillar
Задача предложена пользователем unprost.
Рассмотрим три случая.
h1 + 8a ≥ h2 — в этом случае Гусеница заберётся на яблоко тот же день, поэтому ответ равен 0.
Первой условие не выполнено и a > b — в этом случае гусеница никогда не сможет забраться на яблоко, поскольку она это не сделает в первый день, а после каждой ночи она будет оказываться ниже начала прошлого дня.
Если первые два условия не выполнены, легко видеть, что ответ равен
.
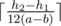Также эту задачу можно было сдать простым моделированием, поскольку высоты и скорости были небольшими.
Сложность: O(1).
652B - z-sort
Задача предложена пользователем Smaug.
Легко видеть, что для любого массива можно осуществить z-сортировку. Пусть в массиве всего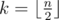 
чётных позиций. Тогда можно на этих позициях расставить наибольшие k элементов массива. Очевидно после этого массив окажется z-отсортированным.
Сложность: O(nlogn).
652C - Foe Pairs
Эта одна из задач предложенных пользователями Bayram Berdiyev bayram, Allanur Shiriyev Allanur, Bekmyrat Atayev Bekmyrat.A.
Предподсчитаем сначала для каждого числа x его позицию posx в перестановке. Это легко сделать за линейное время. Теперь рассмотрим некоторую враждебную пару (a, b) (можно считать, что posa < posb). Запомним для каждого числа a самую левую позицию posb такую, что (a, b) образуют враждебную пару. Обозначим эту величину za. Теперь будем идти по перестановке справа налево и поддерживать позицию rg наибольшего корректного интервала с левым концом в текущей позиции перестановки lf. Значение rg пересчитывается следующим образом: rg = min(rg, z[lf]). Соответсвенно к ответу на каждой итерации нужно прибавлять величину rg - lf + 1.
Сложность: O(n).
652D - Nested Segments
Задачу предложил Алексей Дергунов dalex.
Эта задача является стандартной двумерной задачей, которая решается с помощью одномерной структуры данных. Абсолютно аналогично решаются многие другие задачи (например, поиск наибольшей по весу цепочки точек на плоскости такой, что у каждой следующей точки обе координаты больше, чем у предыдущей). Запишем задачу формально для всех i нам нужно посчитать, количество индексов j, что выполнены следующие условия: ai < aj и bj < aj. Отсортируем все отрезки по левому концу справа налево. И в некоторой структуре данных (удобнее всего здесь использовать дерево Фенвика) будем поддерживать правые концы уже обработанных отрезков (с большим левым концом, чем у текущего отрезка). Тогда для текущего отрезка ответом является сумма на префиксе его правого конца.
Таким образом, от одной размерности задачи (от условия ai < aj) мы избавились с помощью сортировки и обработки отрезков справа налево. А от второй размерности (условия bj < aj) мы избавились использованием структуры данных (взятием суммы на префиксе).
Сложность: O(nlogn).
652E - Pursuit For Artifacts
Задачу предложил Алексей Дергунов dalex.
Компонентой рёберной двусвязности в неориентированном графе называется наибольшее по включению множество вершин такой, что между любой парой вершин существует два рёберно-неперескающихся пути. Рассмотрим граф в котором вершинами являются компоненты рёберной двусвязности исходного графа. Легко видеть, что этот граф является деревом (если бы в нём был цикл, то компоненты цикла образовывали бы одну компоненту двусвязности). Поскольку рёбра исходного графа разрушаются после прохождения по ним, мы не можем перейдя по ребру этого дерева вернуться назад (поскольку это дерево).
Рассмотрим компоненты двусвязности в которые попали вершины a и b. Обозначим их A и B. Утверждение: ответ YES если и только, если на пути в дереве между вершинами A и B либо есть ребро дерева с артефактом, либо есть компонента содержащая внутри себя ребро с артефактом. Легко видеть, что утверждение верно: если такое ребро есть, то мы либо пройдём по нему пока будем идти по дереву из A в B, либо можем пройти по нему внутри компоненты (ведь внутри компоненты между каждой парой вершин есть два рёберно-непересекающихся пути). Обратное также легко непосредственно проверить.
Одним из способов выделить компоненты рёберной двусвязнсти является следующий:
Ориентируем исходный неориентированный граф по обходу в глубину (для каждого ребра запомним в каком направлении мы впервые захотели пройти по нему).
Выделим в этом ориентированном графе компоненты сильной связности.
Утверждение: компоненты сильной связности нового графа будут совпадать с компоненты рёберной двусвязности исходного графа.
Также в этой задаче можно было заметить, что рёбрами дерева будут мосты (мосты в смысле теории графов, а не легенды из условия). Поэтому для решения задачи достаточно выделить мосты в графе.
Сложность: O(n + m).
652F - Ants on a Circle
Задача предложена пользователем Lewin Gan Lewin.
Наблюдение 1: если для нас муравьи неразличимы, можно считать, что никаких столкновений не происходит, а муравьи просто проходят друг через друга. Таким образом, мы можем легко узнать положения всех муравьёв в конце, но мы не можем сказать какой муравей где находится.
Наблюдение 2: относительный порядок муравьёв никогда не меняется.
Таким образом для решения задачи нам достаточно определить положения хотя бы одного муравья по прошествии t единиц времени.
Будем решать эту задачу следующим образом:
Рассмотрим положения муравьёв по прошествии m единиц времени. Легко видеть согласно первого наблюдения, что положения муравьёв остнутся исходными, но порядок изменится (произойдёт циклический сдвиг порядка). Найдём этот циклический сдвиг sh и применим его
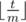раз.После этого останется
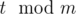единиц времени.
Таким образом, задача свелась к тому, чтобы промоделировать процесс для одного муравья за время m и за время 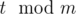. Заметим, что за промежуток времени не больший m один фиксированный муравей не может столкнуться с другим муравьём более двух раз. Таким образом, если мы будем игнорировать столкновения всех остальных муравьёв кроме фиксированного всего произойдёт не более 2n столкновений.
Давайте моделировать этот процесс с помощью двух очередей муравьёв идущих влево и вправо. Каждый раз мы должны брать в очереди противоположного направления первого муравья, обрабатывать столкновение и кидать его в конец очереди другого направления.
Сложность: O(nlogn).
