Update : added another method to code this technique (easy to code but n log ^ 2).

Update 2 : added another method to code this technique (easy to code and n log).

Update 3 : bugs in style 2 have fixed. And 2 new problems added.

Update 4 (15 August 2016) : A new problem (Sgu507) added to list.

Update 5 (20 September) : 2 new problems (291E - Tree-String Problem, 716E - Digit Tree) added to list.

Update 6 (6 December) : My invented style and 741D - Arpa’s letter-marked tree and Mehrdad’s Dokhtar-kosh paths added to list.

Hi!

Most of people know about dsu but what is the "dsu on tree" ?

In Iran, we call this technique "Guni" (the word means "sack" in English), instead of "dsu on tree".

I will explain it and post ends with several problems in CF that can be solved by this technique.

What is the dsu on tree?

With dsu on tree we can answer queries of this type:

How many vertices in subtree of vertice v has some property in O(n lg n) time (for all of the queries).

For example:

Given a tree, every vertice has color. Query is how many vertices in subtree of vertice v are colored with color c?

Lets see how we can solve this problem and similar problems.

First, we have to calculate size of subtree of every vertice. It can be done with simple dfs:

int sz[maxn];
void getsz(int v, int p){
    sz[v] = 1;  // every vertice has itself in its subtree
    for(auto u : g[v])
        if(u != p){
            getsz(u, v);
            sz[v] += sz[u]; // add size of child u to its parent(v)
        }
}

Now we have size of subtree of vertice v in sz[v].

The naive method for solving that problem is this code(that works in O(N ^ 2) time)

int cnt[maxn];
void add(int v, int p, int x){
    cnt[ col[v] ] += x;
    for(auto u: g[v])
        if(u != p)
            add(u, v, x)
}
void dfs(int v, int p){
    add(v, p, 1);
    //now cnt[c] is the number of vertices in subtree of vertice v that has color c. You can answer the queries easily.
    add(v, p, -1);
    for(auto u : g[v])
        if(u != p)
            dfs(u, v);
}

Now, how to improve it? There are several styles of coding for this technique.

1. easy to code but .

map<int, int> *cnt[maxn];
void dfs(int v, int p){
    int mx = -1, bigChild = -1;
    for(auto u : g[v])
       if(u != p){
           dfs(u, v);
           if(sz[u] > mx)
               mx = sz[u], bigChild = u;
       }
    if(bigChild != -1)
        cnt[v] = cnt[bigChild];
    (*cnt[v])[ col[v] ] ++;
    for(auto u : g[v])
       if(u != p && u != bigChild){
           for(auto x : *cnt[u])
               (*cnt[v])[x.first] += x.second;
       }
    //now (*cnt)[c] is the number of vertices in subtree of vertice v that has color c. You can answer the queries easily.

}

2. easy to code and .

vector<int> *vec[maxn];
int cnt[maxn];
void dfs(int v, int p, bool keep){
    int mx = -1, bigChild = -1;
    for(auto u : g[v])
       if(u != p && sz[u] > mx)
           mx = sz[u], bigChild = u;
    for(auto u : g[v])
       if(u != p && u != bigChild)
           dfs(u, v, 0);
    if(bigChild != -1)
        dfs(bigChild, v, 1), vec[v] = vec[bigChild];
    vec[v]->push_back(v);
    cnt[ col[v] ]++;
    for(auto u : g[v])
       if(u != p && u != bigChild)
           for(auto x : *vec[u]){
               cnt[ col[x] ]++;
               vec[v] -> push_back(x);
           }
    //now (*cnt)[c] is the number of vertices in subtree of vertice v that has color c. You can answer the queries easily.
    // note that in this step *vec[v] contains all of the subtree of vertice v.
    if(keep == 0)
        for(auto u : *vec[v])
            cnt[ col[u] ]--;
}

3. heavy-light decomposition style .

int cnt[maxn];
bool big[maxn];
void add(int v, int p, int x){
    cnt[ col[v] ] += x;
    for(auto u: g[v])
        if(u != p && !big[u])
            add(u, v, x)
}
void dfs(int v, int p, bool keep){
    int mx = -1, bigChild = -1;
    for(auto u : g[v])
       if(u != p && sz[u] > mx)
          mx = sz[u], bigChild = u;
    for(auto u : g[v])
        if(u != p && u != bigChild)
            dfs(u, v, 0);  // run a dfs on small childs and clear them from cnt
    if(bigChild != -1)
        dfs(bigChild, v, 1), big[bigChild] = 1;  // bigChild marked as big and not cleared from cnt
    add(v, p, 1);
    //now cnt[c] is the number of vertices in subtree of vertice v that has color c. You can answer the queries easily.
    if(bigChild != -1)
        big[bigChild] = 0;
    if(keep == 0)
        add(v, p, -1);
}

4. My invented style .

This implementation for "Dsu on tree" technique is new and invented by me. This implementation is easier to code than others. Let st[v] dfs starting time of vertex v, ft[v] be it's finishing time and ver[time] is the vertex which it's starting time is equal to time.

int cnt[maxn];
void dfs(int v, int p, bool keep){
    int mx = -1, bigChild = -1;
    for(auto u : g[v])
       if(u != p && sz[u] > mx)
          mx = sz[u], bigChild = u;
    for(auto u : g[v])
        if(u != p && u != bigChild)
            dfs(u, v, 0);  // run a dfs on small childs and clear them from cnt
    if(bigChild != -1)
        dfs(bigChild, v, 1);  // bigChild marked as big and not cleared from cnt
    for(auto u : g[v])
	if(u != big[v])
	    for(int p = st[u]; p < ft[u]; p++)
		cnt[ col[ ver[p] ] ]++;
    //now cnt[c] is the number of vertices in subtree of vertice v that has color c. You can answer the queries easily.
    if(keep == 0)
        add(v, p, -1);
}

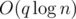But why it is ? You know that why dsu has time (for q queries); the code uses same method. Merge smaller to greater.

If you have heard heavy-light decomposition you will see that function add will go light edges only, because of this, code works in time.

Any problems of this type can be solved with same dfs function and just differs in add function.

Hmmm, this is what you want, problems that can be solved with this technique:

(List is sorted by difficulty and my code for each problem is given, my codes has heavy-light style)

600E - Lomsat gelral : heavy-light decomposition style : 14607801, easy style : 14554536. I think this is the easiest problem of this technique in CF and it's good to start coding with this problem.

570D - Tree Requests : 17961189 Thanks to Sora233; this problem is also good for start coding.

Sgu507 This problem is also good for start.

246E - Blood Cousins Return : 15409328

208E - Blood Cousins : 16897324

291E - Tree-String Problem : See bhargav104's comment below : link.

343D - Water Tree : 15063078 Note that problem is not easy and my code doesn't use this technique (dsu on tree), but my friend, AmirAz 's solution to this problem uses this technique : 14904379.

375D - Tree and Queries : 15449102 Again note that problem is not easy :)).

716E - Digit Tree : 20776957 A hard problem. Also can be solved with centroid decomposition.

741D - Arpa’s letter-marked tree and Mehrdad’s Dokhtar-kosh paths : A hard problem. You must be very familiar with Dsu on tree to solve it.

For persian users there is another problem in Shaazzz contest round #4 (season 2016-2017) problem 3 that is very hard problem with this technique.

If you have another problems with this tag, give me to complete the list :)).

And after all, special thanks from PrinceOfPersia who taught me this technique.