678A - Johny Likes Numbers
The problem was suggested by Abdrakhman Ismail bash.
We should find minimal x, so x·k > n. Easy to see that 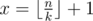 . To learn more about floor/ceil functions I reccomend the book of authors Graham, Knuth, Patashnik "Concrete Mathematics". There is a chapter there about that functions and their properties.
. To learn more about floor/ceil functions I reccomend the book of authors Graham, Knuth, Patashnik "Concrete Mathematics". There is a chapter there about that functions and their properties.
Complexity: O(1).
678B - The Same Calendar
The problem was suggested by Arthur Jaworski KingArthur.
Two calendars are same if and only if they have the same number of days and starts with the same day of a week. So we should simply iterate over years and maintain the day of a week of January, 1st (for example). Easy to see that the day of a week increases by one each year except of the leap years, when it increases by two.
Complexity: O(1) — easy to see that we will not iterate more than some small fixed constant times.
678C - Joty and Chocolate
The problem was suggested by Sheikh Monir skmonir.
Easy to see that we can paint with both colours only tiles with the numbers multiple of lcm(a, b). Obviously that tiles should be painted with more expensive colour. So the answer equals to  .
.
Complexity: O(log(max(a, b))).
678E - Another Sith Tournament
The problem was suggested and prepared by Alexey Dergunov dalex.
Let's solve the problem using dynamic programming. zmask, i — the maximal probability of Ivans victory if the siths from the mask already fought and the i-th sith left alive. To calculate that DP we should iterate over the next sith (he will fight against the i-th sith): 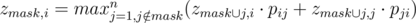 .
.
Time complexity: O(2nn2).
Memory complexity: O(2nn).







