678A - Johny Likes Numbers
Задачу предложил Әбдірахман Исмаил bash.
Нам нужно найти минимальное x, что x * k > n. Легко видеть, что 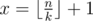 . Для подробного знакомства с математическими функциями пола и потолка я рекомендую книгу авторов Грэхем, Кнут, Паташник "Конкретная математика". В этой книге есть отдельная глава, посвящённая этим функциям и их свойствам.
. Для подробного знакомства с математическими функциями пола и потолка я рекомендую книгу авторов Грэхем, Кнут, Паташник "Конкретная математика". В этой книге есть отдельная глава, посвящённая этим функциям и их свойствам.
Сложность: O(1).
678B - The Same Calendar
Задачу предложил Артур Яворски KingArthur.
Два календаря совпадают если и только, если в них одинаковое количество дней и они начинаются с одного дня недели. Таким образом, достаточно было просто перебрать следующий год, поддерживая первый день недели в году. На самом деле день недели каждый год увеличивается на единицу. Исключением являются високосные годы, когда день недели увеличивается на два.
Сложность: O(1) — легко видеть, что количество итерация не превосходит небольшой константы.
678C - Joty and Chocolate
Задачу предложил Sheikh Monir skmonir.
Легко видеть, что в оба цвета мы можем покрасить доски с номерами кратными lcm(a, b) — НОК чисел a и b. Очевидно, что эти доски выгоднее красить в более дорогой цвет. Таким образом, ответ равен: 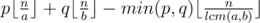 .
.
Сложность: O(1).
678D - Iterated Linear Function
Задачу предложил Zi Song Yeoh zscoder.
В этой задаче можно было вывести формулу в качестве ответа: для этого нужно было посчитать сумму геометрической прогрессии. Далее формулу было легко посчитать с помощью бинарного возведения в степень.
Я опишу более сложное, но более общее решение. Если у нас есть некоторый набор переменных, который пошагово пересчитывается друг через друга с помощью линейной функции, то можно применить бинарное возведение в степень матрицы. Итак, в нашей задаче переменная была одна x. Новая переменная x' получалась по формуле A·x + B. Рассмотрим матрицу z = [[A, B], [0, 1]] и вектор v = [x, 1]. Умножим z на v слева. Легко видеть, что получится вектор v' = [x', 1]. Таким образом, чтобы сделать n итераций, мы просто должны n раз умножить слева матрицу z на вектор v. В силу свойства ассоциативности операции умножения матриц перемножение мы можем сделать бинарно.
В качестве упражнения можете попробовать выписать самостоятельно матрицу для чисел Фиббоначи и научиться их быстро считать. Под спойлером матрица и вектор.
Сложность: O(logn).
678E - Another Sith Tournament
Задачу предложил Алексей Дергунов dalex.
Давайте решать задачу динамикой. zmask, i — наибольшая вероятность выиграть Ивану, если джедаи из маски mask уже хоть раз сражались, а в живых остался только i-й джедай. Для подсчёта динамики переберём следующего джедая (ему придётся сражаться против i-го джедая): 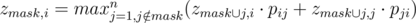 .
.
Сложность по времени: O(2nn2).
Сложность по памяти: O(2nn).







