Author:danilka.pro.
Developed:I_Love_Tina,ThatMathGuy
We can try out all of the possible starting digits, seeing if we will go out of bounds by repeating the same movements. If it is valid and different from the correct one, we output "NO", otherwise we just output "YES".
Author:danilka.pro,I_Love_Tina
Developed:I_Love_Tina,ThatMathGuy
We can build a complete graph where the cost of going from point i to point j if |i - j| if ai! = j and 1 if ai = j.The we can find the shortest path from point 1 to point i.One optimisation is using the fact that there is no need to go from point i to point j if j ≠ s[i],j ≠ i - 1,j ≠ i + 1 so we can add only edges (i, i + 1),(i, i - 1),(i, s[i]) with cost 1 and then run a bfs to find the shortest path for each point i.
You can also solve the problem by taking the best answer from left and from the right and because ai ≤ ai + 1 then we can just iterate for each i form 1 to n and get the best answer from left and maintain a deque with best answer from right.
Complexity is O(N).
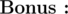 What if you have Q queries Q ≤ 2 × 105 of type (xi, yi) and you have to answer the minimal distance from xi to yi.
What if you have Q queries Q ≤ 2 × 105 of type (xi, yi) and you have to answer the minimal distance from xi to yi.
Author:danilka.pro,I_Love_Tina
Developed:I_Love_Tina,ThatMathGuy
Suppose we want to find the number of ways for a fixed n.
Let a, b, c, d ( 0 < a < b < c < d ≤ n ) be the number of chocolates the thieves stole. By our condition, they have the form b = ak, c = ak2, d = ak3,where k is a positive integer. We can notice that 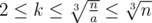 , so for each k we can count how many a satisfy the conditions 0 < a < ak < ak2 < ak3 ≤ n, their number is
, so for each k we can count how many a satisfy the conditions 0 < a < ak < ak2 < ak3 ≤ n, their number is 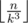 . Considering this, the final answer is
. Considering this, the final answer is 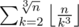 .
.
Notice that this expression is non-decreasing as n grows, so we can run a binary search for n.
Total complexity: Time ~ 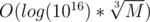 , Space: O(1).
, Space: O(1).
Author:I_Love_Tina
Developed:I_Love_Tina,ThatMathGuy
First of all it is easy to see that if we fix l then have 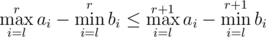 . So we can just use binary search to find the smallest index rmin and biggest index rmax that satisfy the equality and add rmax - rmin + 1 to our answer. To find the min and max values on a segment [l, r] we can use a simple Segment Tree or a Range-Minimum Query data structure.
. So we can just use binary search to find the smallest index rmin and biggest index rmax that satisfy the equality and add rmax - rmin + 1 to our answer. To find the min and max values on a segment [l, r] we can use a simple Segment Tree or a Range-Minimum Query data structure.
The complexity is  time and
time and  space.
space.
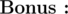 What if you need to count (l1, r1, l2, r2), 1 ≤ l1 ≤ r1 ≤ n, 1 ≤ l2 ≤ r2 ≤ n and
What if you need to count (l1, r1, l2, r2), 1 ≤ l1 ≤ r1 ≤ n, 1 ≤ l2 ≤ r2 ≤ n and 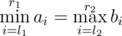 .
.
Author:I_Love_Tina
Developed:I_Love_Tina,ThatMathGuy
Let define the following propriety:if the point i is intersected by p segments then in our sum it will be counted 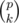 times,so our task reduce to calculate how many points is intersected by i intervals 1 ≤ i ≤ n.Let dp[i] be the number of points intersected by i intervals.Then our answer will be
times,so our task reduce to calculate how many points is intersected by i intervals 1 ≤ i ≤ n.Let dp[i] be the number of points intersected by i intervals.Then our answer will be 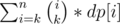 . We can easily calculate array dp using a map and partial sum trick.
. We can easily calculate array dp using a map and partial sum trick.
The complexity and memory is  and O(n).
and O(n).
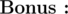 what if
what if 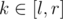 where l, r are given in input.
where l, r are given in input.
I'm really sorry for problem A because it was harder than ussually.





