691A - Fashion in Berland
The problem was suggested and prepared by Arthur Jaworski KingArthur.
In this problem you should simply check the conditions from the problem statement.
Complexity: O(n).
691B - s-palindrome
The problem was suggested by Nikita Melnikov nickmeller.
In this problem you should simply find the symmetric letters by picture and also observe that the pairs (b, d) and (p, q) is the symmteric reflections.
Complexity: O(n).
691C - Exponential notation
The problem was suggsted by user blowUpTheStonySilence.
This is an implementation problem. You should do exactly what is written in the problem statement. On my mind the simplest way is to find the position of the first not zero digit and the position of the dot. The difference between that positions is the value of b (if the value is positive you should also decrease it by one).
Complexity: O(n).
691D - Swaps in Permutation
The problem was suggested by Zi Song Yeoh zscoder.
Consider a graph with n vertices whose edges is the pairs from the input. It's possible to swap any two values with the positions in some connected component in that graph. So we can sort the values from any component in decreasing order. Easy to see that after sorting the values of each component we will get the lexicographically maximal permutation.
Complexity: O(n + m).
691E - Xor-sequences
The problem was suggested by Zi Song Yeoh zscoder.
Let zij be the number of xor-sequences of length i with the last element equal to aj. Let gij be equal to one if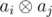 
contains the number of ones in binary presentation that is multiple of three. Otherwise let gij be equal to zero. Consider a vectors zi = {zij}, zi - 1 = {zi - 1, j} and a matrix G = {gij}. Easy to see that zi = G × zi - 1. So zn = Gnz0. Let's use the associative property of matrix multiplication: at first let's calculate Gn with binary matrix exponentiation and then multiply it to the vector z0.
Complexity: O(n3logk).
691F - Couple Cover
The problem was suggested by Michael Kirsche mkirsche.
Let's count the number of pairs with multiple less than p. To get the number of not less pairs we should sumply subtract from n·(n - 1) the number of less pairs. Let cnti be the number of values in a equal to i and zj be the number of pairs from a with the multiple equal to j. To calculate the values from z we can use something like Eratosthenes sieve: let's iterate over the first multiplier a and the multiple of it b = ka and increment zb by the value cnta·cntk. After calculating the array z we should calculate the array of its partial sums and find the number of less pairs in O(1) time.
Complexity: O(n + XlogX), where X is the maximal value in p.
