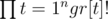Hi guys, given that the tutorial didn't include any solution for problem F of that round, I decided to explain my solution because I'm sure the problem was really interesting.

First step

Let's denote f as the inverse map of p.

We can easily notice that the key is about looking at the prime factors of the numbers because the condition (i, j) = 1 iff (p_i, p_j) = 1 is equal to (i and j don't share any prime factor) iff (p_i and p_j don't share any prime factor). So, we will divide the numbers into some groups(which are not necessarily disjoint) such that any tow numbers in the same group share a common prime factor. Then, let G_q be the group of all numbers between 1 and n which are divisible by q. In addition, we will keep a group G₁ = { 1 }, because as we know 1 is coprime with any number and it also doesn't have any prime factor.

Now, these groups are interesting because p_x and p_y will be in some group G_r for any numbers x and y in G_q (r depends on x and y, obviously). However, we could show that p(G_q) = G_r for any prime number q. The proof consists on noticing that if p_q belongs to some group G_r then (f(r) , q) is not 1(because r and p_q are in the same group) then f(r) belongs to G_q. Now, if y belongs to G_q then (y, x) is not 1 and then (p_y, r),so p_y belongs to G_r. Then, p(G_q) G_r. Analogously, we can prove that f(G_r) G_q and that completes the proof.(We used that q is prime, but this proof also works if q = 1).

So, we have proved that any q is mapped into some other r(where q and r are the indexes of the groups i.e. primes or 1). And this is basically all the solution because the next step will be about proving that if h is a bijective map which takes indexes into indexes of groups, then p_x = y is a feasible permutation , where all the prime factors of y are the images by h of the prime factors of x(here we are considering that the only factor of 1 is 1).

Second step

Claim: The only feasible permutations are those which satisfies p_x = y where all the prime factor of y are the images by h of the prime factors of x.

It is fairly easy to prove that if p satisfies the condition stated before, then p satisfies (i , j) = 1 iff (p_i, p_j) = 1

Now, we will prove that the condition is necessary. It is clear that h needs to be bijective(a group can only be mapped into one group).If q is any prime factor of x then h(q) is a prime factor of p_x(because of First Step). If r is any prime factor of y then the preimage of r is a prime factor of the preimage of p_x(This is also the first step, but considering the inverse of h instead of h). (Again, the proof remains true for the case q = 1).

Conclusion

In summary, we have proved that any bijective map h and any permutation satisfying Claim will turn out to be a feasible solution for p. So, the answer will be (#of feasible h)(# number of feasible p given h)

Number of feasible h is the number of ways to assign a prime r to any other prime q(here we will say 1 is "prime"), but those h are not only random bijective maps between primes, we should remember that the assignment satisfies that h(q) = r iff p(G_q) = G_r, so it is necessary that (number of elements of G_r) = (number of elements of G_q). Then, in the implementation, we will compute (number of elements of every group G_s) which is 1 if s = 1 and n/s if s is a prime greater than 1.(Think about it for a while if it's not clear at the beginning). Then, we should know how many groups have a fixed numbers of elements , say there are gr[t] groups which have t elements. Provided of this notation, the number of maps h will be