Since the official editorial is yet to be released and people are starting to ask for editorial, I decide to write this problem analysis and hopefully this may help the situation. =]
Sorry for my bad English if I made some grammatical mistakes.
732A. Buying a shovel
We could simulate the buying process — just buy until you can buy without change.
As the problem statement have already stated, you can always buy 10 shovels without change, so there is at most 10 iterations.
732B. Cormen — The Best Friend Of a Man
Iterate the days from left to right, and increase the days greedily on the right to fulfill the requirement. Take a look at this figure if you don't understand why this doesn't know why this works.
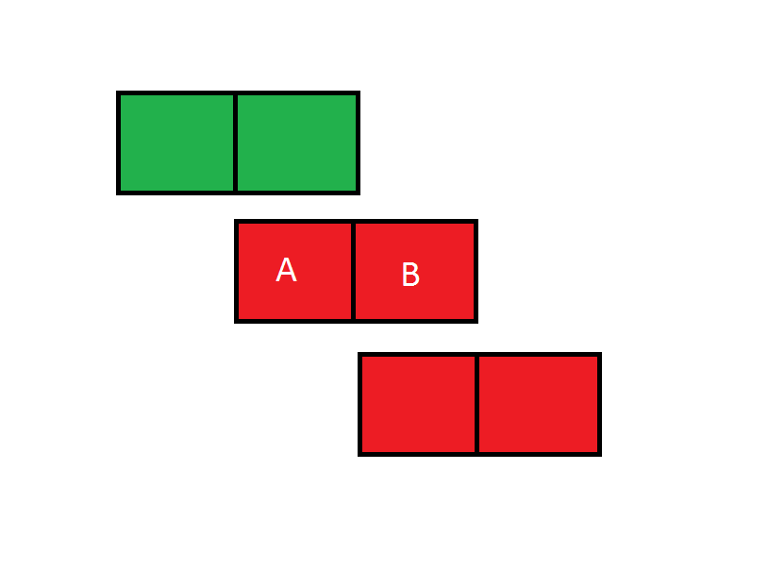
Let's say we are deciding to whether increase the days on A or B to make the total walks on those days become >= k. As we are iterating from left to right the blocks to the left are guaranteed to have already fulfilled the requirement. You can see that placing extra walks on day A will be less beneficial, as placing extra walks on day B could possibly help out the block day B and day B+1.
732C. Sanatorium
Let's start from scratch, assume that we start and end our vacation before, what is the solution? Let MAX be the most ate meal throughout the vacation, we have to stay at least MAX days to eat enough meals, so the answer is 3*MAX — (sum of meals).
Now we come back to our question — how about if can start and end at anytime? With a little bit of imagination you can see that we could have an extra (or have one less) meal of any combination. As we have discovered before, the solution is 3*MAX — (sum of meals), so we have to greedily reduce the number of MAX to find out the minimal solution.





