Here's the problem (IMO 2013 Problem 1): Assume that k and n are two positive integers. Prove that there exist positive integers m1, ... , mk such that 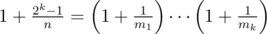 .
.
There is an inductive proof, which is generally the more popular solution, but I would like to demonstrate a solution that relates this problem to a well-known data structure: the segment tree.
Think:
Here's a generalization, which is much easier once you've found the segtree solution to the above problem. Assume that k and n are two positive integers. Prove that there exist positive integers m1, ... , mk such that 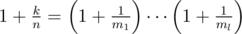 , where l is an integer and l ≤ 2 × ceil(log2(k / 2 + 1)).
, where l is an integer and l ≤ 2 × ceil(log2(k / 2 + 1)).
Challenge: Implement the two variants of the problem. In the generalization, you are given k and n, and you are required to output an array that consists of m1, m2, ..., ml.



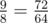 . Hmmm now how could we do this?
. Hmmm now how could we do this? 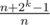 to a range
to a range 

