We have a tree with n (2 ≤ n ≤ 1000) nodes and we need to find k (1 ≤ k ≤ 100 and k ≤ n - 1) vertices such that the path going through all of these vertices has the maximum length.

Note:

• The path should start at vertex 1 and finish also at vertex 1.
• The algorithm has to return just the length of the maximum path (the path itself is not needed).
• The weight for the edge has following restrictions: 0 ≤ w ≤ 100000.

Let's say we have the following tree with n = 5 vertices: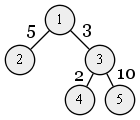

We need to find k = 3 vertices which will give us the longest path.

For this tree the maximal path is the following:
1 ⟶ 5 ⟶ 2 ⟶ 4 ⟶ 1

It has the total length of 13 + 18 + 10 + 5 = 46.
So, for that particular tree we have to print 46 as our result.

I came up with a following greedy/dp-like solution. First we solve the problem for k = 1 and we remember this solution in a linked list 1 ⟶ v ⟶ 1. After that we try to solve the problem for k = 2 by trying all of the remaining n - 2 vertices and insert it in the current path: 1 ⟶ u ⟶ v ⟶ 1 and 1 ⟶ v ⟶ u ⟶ 1. After going through all of the vertices we choose the one which gave us the best result. Then we proceed to solve k = 3.

The problem is that it looks like this solution is not correct, because it fails the tests for this problem. I cannot prove that my solution is correct and I cannot disprove it. All I managed to do is to generate millions of different random trees and in all of these cases my clever solution matched bruteforce solution.

For now all my effort is directed towards generating a counter example in which my method will fail, but if it is correct I'd be glad to see the reasoning why is it correct.