One of my friend recently asked me the following problem:
"Given an array a1, a2, ..., an and a number K (n < = 105, ai < = 109). Is there a way split the array into K disjoint sub-arrays (don't have to be contiguous) such that sum of each sub-array is equal to each other (and equal to 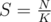 )?"
)?"
My teacher came up with the following greedy solution: for each sub-array, keep choosing the maximum number such that sum of sub-array with that number is still smaller or equal to S. When it's impossible to add more number from a to this sub-array, check if the current sum is equal to S.
However, both my teacher and me are unable to neither prove the correctness of the solution nor find a counter-example for it. Is this greedy solution always optimal? How to prove (or disprove) it? Thanks in advance.





