798A - Mike and palindrome
Let cnt be the number of 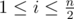 such that si ≠ sn - i + 1.
such that si ≠ sn - i + 1.
If cnt ≥ 2 then the answer is NO since we must change more than 1 character.
If cnt = 1 then the answer is YES.
If cnt = 0 and n is odd answer is YES since we can change the character in the middle, otherwise if n is even the answer is NO because we must change at least one character.
Complexity is O(|s|).
798B - Mike and strings
First of all, you must notice that the operation of removing the first character and appending it to the left is equivalent to cyclically shifting the string one position to the left.
Let's denote by dpi, j the smallest number of operations for making the first i strings equal to string si moved j times.
Let f(i, j) be the the string si moved j times,then 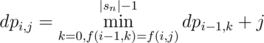 .
.
The answer is min(dpn, 0, dpn, 1, ..., dpn, |sn| - 1).
The complexity is O(|S|3 × n).
798C - Mike and gcd problem
First of all, the answer is always YES.
If 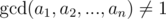 then the answer is 0.
then the answer is 0.
Now suppose that the gcd of the sequence is 1. After we perform one operation on ai and ai + 1, the new gcd d must satisfy d|ai - ai + 1 and d|ai + ai + 1  d|2ai and d|2ai + 1. Similarly, because d is the gcd of the new sequence, it must satisfy d|aj, j ≠ i, i + 1.
d|2ai and d|2ai + 1. Similarly, because d is the gcd of the new sequence, it must satisfy d|aj, j ≠ i, i + 1.
Using the above observations we can conclude that  , so the gcd of the sequence can become at most 2 times bigger after an operation. This means that in order to make the gcd of the sequence bigger than 1 we need to make all numbers even. Now the problem is reduced to the following problem:
, so the gcd of the sequence can become at most 2 times bigger after an operation. This means that in order to make the gcd of the sequence bigger than 1 we need to make all numbers even. Now the problem is reduced to the following problem:
Given a sequence v1, v2, ... , vn of zero or one,in one move we can change numbers vi, vi + 1 with 2 numbers equal to 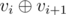 . Find the minimal number of moves to make the whole sequence equal to 0.
. Find the minimal number of moves to make the whole sequence equal to 0.
It can be proved that it is optimal to solve the task for consecutive ones independently so we divide the array into the minimal number of subarrays full of ones, if their lengths are s1, s2, ... , st,the answer is  .
.
Complexity is 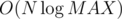 .
.





