798A - Майк и палиндром
Let cnt be the number of 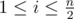 such that si ≠ sn - i + 1.
such that si ≠ sn - i + 1.
If cnt ≥ 2 then the answer is NO since we must change more than 1 character.
If cnt = 1 then the answer is YES.
If cnt = 0 and n is odd answer is YES since we can change the character in the middle, otherwise if n is even the answer is NO because we must change at least one character.
Complexity is O(|s|).
798B - Майк и строки
First of all, you must notice that the operation of removing the first character and appending it to the left is equivalent to cyclically shifting the string one position to the left.
Let's denote by dpi, j the smallest number of operations for making the first i strings equal to string si moved j times.
Let f(i, j) be the the string si moved j times,then 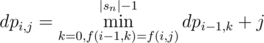 .
.
The answer is min(dpn, 0, dpn, 1, ..., dpn, |sn| - 1).
The complexity is O(|S|3 × n).
798C - Майк и GCD
First of all, the answer is always YES.
If 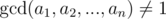 then the answer is 0.
then the answer is 0.
Now suppose that the gcd of the sequence is 1. After we perform one operation on ai and ai + 1, the new gcd d must satisfy d|ai - ai + 1 and d|ai + ai + 1  d|2ai and d|2ai + 1. Similarly, because d is the gcd of the new sequence, it must satisfy d|aj, j ≠ i, i + 1.
d|2ai and d|2ai + 1. Similarly, because d is the gcd of the new sequence, it must satisfy d|aj, j ≠ i, i + 1.
Using the above observations we can conclude that 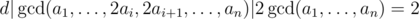 , so the gcd of the sequence can become at most 2 times bigger after an operation. This means that in order to make the gcd of the sequence bigger than 1 we need to make all numbers even. Now the problem is reduced to the following problem:
, so the gcd of the sequence can become at most 2 times bigger after an operation. This means that in order to make the gcd of the sequence bigger than 1 we need to make all numbers even. Now the problem is reduced to the following problem:
Given a sequence v1, v2, ... , vn of zero or one,in one move we can change numbers vi, vi + 1 with 2 numbers equal to 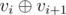 . Find the minimal number of moves to make the whole sequence equal to 0.
. Find the minimal number of moves to make the whole sequence equal to 0.
It can be proved that it is optimal to solve the task for consecutive ones independently so we divide the array into the minimal number of subarrays full of ones, if their lengths are s1, s2, ... , st,the answer is 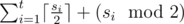 .
.
Complexity is 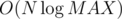 .
.
798D - Майк и распределение
In the beginning, it's quite easy to notice that the condition "2·(ap1 + ... + apk) is greater than the sum of all elements in A" is equivalent to ap1 + ... + apk is greater than the sum of the remaining elements in A.
Now, let's store an array of indices C with Ci = i and then sort it in decreasing order according to array A, that is ACi ≥ ACi + 1.
The complexity is 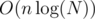 .
.
798E - Майк и код перестановки
Let's consider ai = n + 1 instead of ai = - 1. Let's also define the sequence b, bi = j such that aj = i or bi = n + 1 if there is no such j. Lets make a directed graph with vertices be the indices of the permutation p with edges of type (a, b) representing that pa < pb. If we topologically sort this graph then we can come up with a possible permutation,if S is the topologically sorted graph then we can assign to pSi number i (in other words pSi = i).
But how we can find the edges? First of all there are edges of form (bi, i) if bi ≠ n + 1.For a vertex i he visited all the unmarked vertices j (1 ≤ j < ai, j ≠ i) and you know for sure that for all these j,pj < pi. But how we can check if j was already marked? The vertex j will become marked after turn of vertex bj or will never become unmarked if bj = n + 1. So there is a direct edge from i to j if j = ai or 1 ≤ j < ai, j ≠ i and bj > i.
The main problem is to extract j for a given i in a sub-quadratic time,the solution is segment tree and is based on the fact that each time we want to extract vertex j from all non-visited edges (1 ≤ j < ai,j ≠ i) with maximal bj,if bj < i then there aren't remaining edges.
Complexity and memory are  and O(N).
and O(N).





