Задача A. Письма долгого хранения.

В данной задаче требовалось просто просимулировать описанный в условии процесс. Например, можно в любой структуре данных (массив, очередь, дерево) поддерживать множество ещё не обработанных писем и по очереди рассматривать все моменты времени. При рассмотрении момент времени x сначала проверяем, есть ли новое входящее письмо, и, если да, то добавляем его в структуру. Далее проверяем, не наступило ли хотя бы одно из условий, при которых Бомбослава разбирает почту. Для симулирования разбора почты вычисляем число k и последовательно вынимаем k наиболее старых писем из структуры. Даже самая простая реализация этого процесса будет работать за время O(nT).

Упражнение: решите задачу за время O(n).

Задача B. Девчата против автомата.

Для начала заметим, что если Дуся и Люся поделят число n на x и n - x, то они получат в качестве сдачи ровно такой же набор банкнот, как если поделят n на x + 5000 и n - x - 5000. Таким образом, достаточно будет только проверить всем способы разбиения, где x проходит диапазон от a до min(a + 5000, n - a). Для каждого способа вычислим сдачу за время O(1) по следующей формуле: если какая-либо из девушек хочет заплатить величину y, то размер полезной сдачи будет (5000k - y) mod 500, где .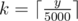

Упражнение: докажите, что достаточно перебрать значения x в диапазоне от a до min(a + 499, n - a) включительно.

Задача C. Эффективный менеджмент возвращается.

Существует множество различных решений данной задачи, и почти любое из них уложится в ограничение по времени, поскольку в ответе будет использовано не более 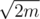команд (упражнение: доказать это утверждение). Данный разбор будет содержать описание одного из возможных линейных решений.

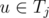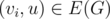Будем добавлять вершины графа по одной. После рассмотрения первых i - 1 вершин (v₁, v₂, ..., v_i - 1) мы будем поддерживать распределение их между k_i командами T₁, T₂, ..., T_ki, так что все указанные в условии задачи ограничения выполнены. При добавлении вершины v_i найдём любую команду T_j, такую что не существует вершины and . Полагая 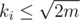это может быть легко реализовано за время 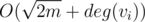просто с использованием массива булевых пометок и проходом по списку соседей вершины. Если подходящего T_j не существует, то положим k_i + 1 = k_i + 1, то есть создадим для данной вершины отдельную команду. На самом деле, нам не требуется использовать факт про то, что количество команд есть 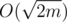, поскольку вместо обнуления булевого массива мы можем использовать массив специальных пометок. За время O(deg(v_i)) расставим пометки всем соединённым с данной вершиной командам, а потом просто пройдём по массиву до тех пор, пока не найдём непомеченную команду. Разумеется, при выполнении этой части будет просмотрено не более deg(v_i) + 1 элементов массива и вообще при добавлении вершины будет сделано O(deg(v_i)) действий. Таким образом, суммарное время работы есть O(n + m).

Задача D. Афера.

Для начала будем несколько иначе воспринимать все ставки. Определим c_i = a_i + b_i, тогда принимая ставку i мы можем считать, что получаем доход b_i и должны будем выплатить c_i в случае наступления соответствующего исхода. Определим A как некоторое подмножество ставок, 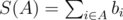, то есть итоговый доход с данного подмножества без учёта возможных выплат. L(A) положим равному суммарным выплатам, если команда проиграет, то есть . Аналогично введём величины D(A) и W(A), тогда гарантированный доход Остапа с подмножества A равен S(A) - max(L(A), D(A), W(A)).

В данном виде пока ещё непонятно как решать задачу, поскольку требуется с одной стороны увеличивать S(A), и минимизировать максимум с другой стороны. Зафиксируем max(L(A), D(A), W(A)) = k, тогда задача звучит как: какова максимальная стоимость по b_i подмножества ставок с исходом "поражение" ("ничья", "победа"), которое можно принять так чтобы сумма их c_i не превосходила k. Соответствующие значения 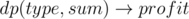можно независимо посчитать для каждого исхода с помощью динамического программирования решающего задачу о рюкзаке. Сложность такого решения будет O(nL), где .

Задача E. Случайная величина моды.

Сперва рассмотрим решение задачи за время O(n²) с помощью динамического программирования. Положим dpleft(i, j) равным оптимальному ожидаемому времени в торговом центре, если Глеб уже обошёл все магазины с i по j включительно и сейчас стоит рядом с магазином i. Аналогично положим dpright(i, j) равным оптимальному ответу если Глеб обошёл магазины с i по j и стоит около магазина j.

Мы не будем приводить всех формул в данном разборе, но, например, dpleft(i, j) может быть вычислено как минимум из двух возможных переходов (в i - 1 или

Unable to parse markup [type=CF_TEX]

,

Для ускорения решения задачи заметим, что если не существует магазинов с p_i = 0, то мы посетим большое количество магазинов с очень маленькой вероятностью, поскольку уже вероятность в один процент, то есть 0.01 является достаточно большой. Вероятность посетить k магазинов с p_i > 0 и всё ещё не найти подходящий плащ составляет 0.99^k, что для k = 5000 составит порядка 1.5·10^- 22. используя что t_i ≤ 1000 и n ≤ 300 000 получаем, что на посещение всего торгового центра потребуется не более 10⁹ секунд, то есть уже при k = 5000 влияние на ответ составит не более 10^- 12. На самом деле, учитывая, что нам разрешается допустить относительную ошибку 10^- 6 достаточно будет k = 3000.

Теперь найдём не более k магазинов с p_i > 0 и i < x и не более k магазинов с p_i > 0 и i > x (то есть слева и справа от стартового). Далее сожмём магазины с p_i = 0 и применим квадратичную динамику. Итоговое время работы составит O(n + k²).

Задача F. Семь раз отмерь, один раз раздели.

Каждой вершине требуется назначить неотрицательное целое число x_v равное номеру итерации описанного в условии процесса, на которой данная вершина будет удалена. По причинам, которые станут понятны читателю в дальнейшем, мы будем считать, что x_v = 0 означает удаление на самой последней итерации, то есть б**о**льшие значение x будут соответствовать более ранним итерациям процесса. Можно показать, что фиксированные значения x_v корректно описывают процесс, если и только если для любых двух вершин u и v, таких что x_u = x_v максимальное значение x_w по всем w лежащим на пути от u до v больше x_u. Другими словами, наличие на любом пути между двумя одинаковыми значениями другого значения, которое больше их обоих, означает, что любые две вершины, удаляемые на одном шаге, будут к этому моменту находиться в разных компонентах.

Выберем любую вершину в качестве корня дерева. Обозначим через C(v) множество непосредственных детей вершины v, а через S(v)~--- поддерево вершины v. Теперь, если в поддереве v уже зафиксирована некоторая корректная расстановка значений x, то нас интересуют только те x_u, 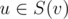, которые ещё никем не перекрыты, то есть на пути от u до вершины корня поддерева (вершины v) нет значения больше x_u. Через d(v, mask) обозначим булево значение, возможно ли так расставить x в поддереве вершины v, чтобы незакрытыми оставались только значения из множества mask. Поскольку благодаря центроидной декомпозиции мы знаем, что величина ответа не превзойдёт 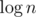, то интересных значений mask не более 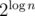, то есть O(n). Значения d(v, mask) можно вычислить если известны d(u, mask) для всех 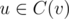за время O(n³) используя следующие соображения (обозначим через u₁, u₂, ... детей из C(v), а через m₁, m₂, ... рассматриваемые в них значения динамики):

1. Значение x_v должно быть больше любого i, которое встречается более чем в одной маске m_i.
2. Значение x_v должно быть равно какому-нибудь i, которое не встречается ни в одной m_i.
3. Если мы положим x_v = i, то все j < i будут равны 0 в m.

Заметим, что согласно описанному выше процессу если маска m₁ является подмаской m₂, то она всегда лучше влияет на ответ, чем m₂. Теперь мы утверждаем, что если рассмотреть минимальное m, такое что d(v, m) = true, то для любой m₁ > m найдётся m₂ подмаска m₁, такая что d(v, m₂) = true. В самом деле, рассмотрим первый (старший) бит i, в котором m и m₁ отличаются. Поскольку m₁ больше m, то в этой позиции у неё будет записано 1, а у m будет записан 0. Если после этого в m вообще нет 1, то она сама является подмаской m₁, в противном случае это означает, что x_v < i. Выставим x_v = i и получим подмаску m₁.

Доказанное выше означает, что достаточно только рассмотреть лексикографически минимальную маску, которую можно получить в каждом из поддеревьев S(v). Для этого будем объединять ответы по всем 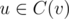используя вышеописанную процедуру. Такое решение может быть легко реализовано за время или даже O(n) при эффективном использовании битовых операций.