Hi. I am having problem trying to solve JOI 2013/2914 — Historical Research. The english problem statement can be found here.

For those who can read Japanese, the editorial can be found here

The input and output data can be found here

My approach is as follows:

We use an additional BST to answer our max product queries and element updates efficiently. Hence, each element of the BST would be <product,element,frequency>.

Let N be the number of elements in our array and Q be the number of queries.

Perform square root decomposition on the queries by breaking them into blocks and sorting them in increasing order of left bound followed by increasing order of right bound. Time-complexity of this operation is O(Q × logQ).

We keep 2 pointers to track the left and right bound of the subarray that we have calculated the element frequency for. Every time we shift the left pointer, we remove the elements from the left side of the window from the BST. Every time we shift the right pointer, we add the new elements in the window to the BST.

Of course, we have to update the product accordingly. Complexity of this operation is 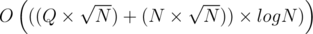. This is because each query can only be in one block. Hence, the left pointer can only move by on each query (i.e. in total) and the right pointer moves by O(N) in every block and we have blocks. Hence, right pointer moves by in total. Each movement incurs an update operation in the BST which is O(logN)

Every time we need to query for