А. Ярмарка оружия [реализация, математика]

Необходимо последовательно сравнить силы наборов, если текущая сила строго больше максимальной предыдущей, то обновляем максимальную и индекс лучшего набора. Вычислить силу набора можно было в нецелых числах как (сумма s_i, j / w_i), или сохранить числитель и знаменатель дроби (sum_smax и w_max) и сравнивая с текущим набором домножить обе части на (w_max·w_i). Не стоит забывать, что суммирование 10⁵ чисел до 10⁹ приведёт к переполнению типа integer.

Код в нецелых числах: O(n)

B. Имённо-фамильный никнейм [перебор, строки]

Любое решение сводится к тому, чтобы максимизировать подстроку в n (ведь чем больше символов мы возьмём из n, тем меньше потребуется из f).

Обозначим длину такой подстроки за k.

1) Наивное решение может проверять все подстроки строки n для поиска максимального k, после чего искать недостающий конец строки в f. Это будет работать за O(q * |n|² + q * |f|) в теории, однако лишь в худшем частном случае, когда множество раз наблюдается значительное совпадение подстроки с первой часть строки s_i (пример: n = " ", f = " ", и все s_i = " ").

Код

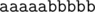2) Подсчитать все возможные подстроки для n за |n|², сложить в set или бор, или подсчитать хеши (это будет работать аналогично set). Теперь для каждого s_i можно последовательно искать k, после чего можно пройтись последовательно по f, узнав, есть ли там оставшиеся |s_i| - k символов. При использовании set или хешей можно также искать k бинарным поиском, укорачивая или удлиняя текущую строку до длины M на каждой итерации и ища ей соответствие в подстроках n. Асимптотики такого решения: \begin{itemize} \item {Для хешей или set: \begin{enumerate} \item если искать k последовательно: O(q * k * log₂(|n|²) + q * |f|) \item бинарным поиском: O(q * log₂(k) * log₂(|n|²) + q * |f|) \end{enumerate} } \item Для бора: O(q * k + q * |f|) \end{itemize}

Код с set, последовательное $k$

Код с set, бинарный поиск по $k$

Код с бором

2) Развернём n, f, и s_i задом наперёд. Тогда нам нужно максимизировать не подстроку, а подпоследовательность в f, в этом единственное отличие от предыдущего варианта. Искать k для подпоследовательности можно только последовательно, после чего нам нужно найти в n подстроку длины |n| - k, для чего опять же следует предподсчитать все возможные подстроки для n за |n|² и сложить их в какую-нибудь структуру. Асимптотика решения: \begin{itemize} \item Для хеша или set: O(q * k + q * log₂(|n|²)) \item Для бора: O(q * k + q * |n|) \end{itemize}