[problem:A]
One can see that in the final set all the elements less than x should exist, x shouldn't exist and any element greater than x doesn't matter so we will count the number of elements less than x that don't exist in the initial set and add this to the answer, If x exists we'll add 1 to the answer because x should be removed .
Problem author : mahmoudbadawy .
Time complexity : O(n+x) .
Solution link (me) : TODO .
Solution link (mahmoudbadawy) : TODO .
[problem:B]
The tree itself is bipartite so we can run a dfs to partition the tree to the 2 sets, We can't add an edge between any 2 nodes in the same set and we can add an edge between any 2 nodes in different sets so let the number of nodes in the left set be l and the number of nodes in the right set be r, The maximum number of edges that can exist is l * r, n - 1 edges already exist so the maximum number of edges to be added is l * r - n + 1.
Problem author : me .
Time complexity : O(n) .
Solution link (me) : TODO .
Solution link (mahmoudbadawy) : TODO .
[problem:C]
There are multiple ideas for this problem, I will mention some of them.
Common things : n = 2, x = 0 is the only case with answer "NO" and PW = 217 .
First solution by me
Let's define a block of integers as 4 consecutive integers where the first one is divisible by 4, The bitwise-xor sum of a block is 0.
proof: let the first integer be x, as x is divisible by 4, 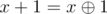 ,
, 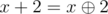 and
and  so the bitwise-xor sum is
so the bitwise-xor sum is 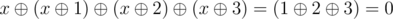
So let's print some blocks and reduce n by 4 until n is 4 or less, Don't print the block that starts with 0 or the block that contains x (You'll know why later) .
Now we want a bitwise-xor sum equals x with n ≤ 4, Let's try to find a set of integers such that for any n ≤ 4 and x, There exists a subset of it with size n that has the bitwise-xor sum x, Try to prove that the set 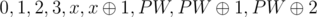 fulfills the condition, You can try all its subsets that has n elements in O(94) or O(9!), We didn't use the block (0, 1, 2, 3) or the block that contains x because we need them in our set.
fulfills the condition, You can try all its subsets that has n elements in O(94) or O(9!), We didn't use the block (0, 1, 2, 3) or the block that contains x because we need them in our set.
Second solution by mahmoudbadawy
First print 1, 2, ..., n - 3 (The first n - 3 positive integers), Let their bitwise-xor sum be y, If x = y You can add PW,PW * 2 and 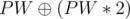 , Otherwise you can add 0,PW and
, Otherwise you can add 0,PW and 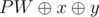 .
.
Handle n = 1 (print x) and n = 2 (print 0 and x) .
Problem author : mahmoudbadawy .
Solution link (me) : TODO .
Solution link (mahmoudbadawy) : TODO .
Your thoughts are welcome in the comments .
[problem:D]
There are also multiple solutions to this problem .
In the editorial we suppose that the answer of some query is the number of correct position which is n-(the hamming distance), For convenience.
Common things : Let zero(l, r) be a function that returns the number of zeros in the interval [l;r] minus the number of ones in it, We can find it in one query after a preprocessing query, The preprocessing query is 1111..., Let its answer be stores in allones, If we made a query with a string full of ones except for the interval [l;r] which will be full of zeros, If this query's answer is cur, zero(l, r) = cur - all, That's because all is the number of ones in the interval plus some trash and cur is the number of zeros in the interval plus the same trash .
First solution by mahmoudbadawy
Let's have a searching interval, initially this interval is [1;n] (The whole string), Let's repeat this until we reach our goal, Let mid = (l + r) / 2 Let's query to get zero(l, mid), If it's equal to r - l + 1, This interval is full of zeros so we can print any index in it as the index with value 0 and continue searching for an index with the value 1 in the interval [mid + 1;r], But if its value is equal to l - r - 1, This interval is full of ones so we can print any index in it as the index with value 1 and continue searching for a 0 in the interval [mid + 1;r], Otherwise we can continue searching for both in the interval [l;mid], Every time the searching interval length must be divided by 2 in any case so we perform O(log(n)) queries .
Second solution by me
Let's send 1111... and let the answer be ans1, Let's send 0111... and let the answer be ans0, We now know the value in the first index (1 if ans1 > ans0, 0 otherwise), We can binary search for the first index where the not-found value exists, which is to binary search on the first value x where zero(2, x) * sign(non - foundbitvalue) ≠ x where sign(y) is 1 if y = 0, - 1 otherwise .





