I've been thinking for one month and I still don't know how to solve this problem:

There is a park of size (A<=100)x(B<=100) (consider it as a grid), with (1, 1) as the top-left corner. There are C<=1000 trees on the park, all of which have distinct locations. You want to place as many VIP lounges on the park as possible, such that every VIP lounge is adjacent to a tree on its top, bottom, left, or right. But because of privacy issues, a VIP lounge cannot be adjacent to another VIP lounge (including diagonally). Note that you cannot place a VIP lounge on a tree.

For example, consider the following park of size 9x7:

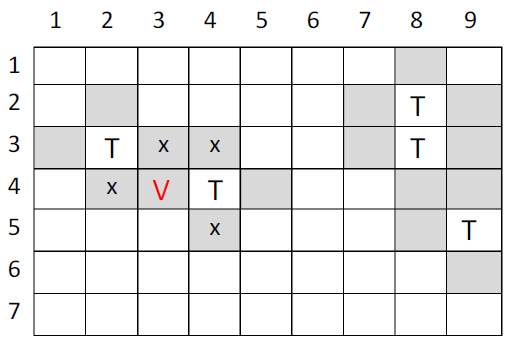
The "T"s represent the trees, the grey shaded areas represent possible locations for VIP lounges. If there were to be a VIP lounge on where the "V" is located, then the "x"s represent the locations where there cannot be VIP lounges.

Sample 1:

Input: T__ ___ T

Output: 3

TV_ ___ VTV

Sample 2:

Input: ______ T___ T_ ____T_ ______

Output: 5

______ VTV___ __T_V_ __V_T_ ____V_

My thoughts:

Finding the maximum independent set of a bipartite graph can be done in polynomial time. Create a graph in which the possible VIP lounge placements are nodes and there are edges between 2 nodes if the 2 VIP lounges are adjacent. The maximum independent set of this graph is the answer. Notice that this graph is quadripartite (all combinations of x, y mod 2). Maybe there is also a way to find the maximum independent set of a quadripartite graph efficiently.