Недавно наткнулся на задачу 803F - Взаимно простые подпоследовательности, в которой требуется найти число таких подпоследовательностей массива, что НОД всех чисел подпоследовательности равен 1. Задача несложная и решается на основе следующих соображений:

1. Число непустых подпоследовательностей массива из k элементов равно 2^k - 1
2. Задачу можно переформулировать так: необходимо отыскать количество подпоследовательностей, для которых не найдется простого числа, делящего все элементы
3. Пусть P — множество простых чисел до 10⁵, а d(x) — число подпоследовательностей, каждый элемент которых кратен x. Если m(x) — число элементов массива, кратных x, то в соответствии с п. 1 имеем d(x) = 2^m(x) - 1
4. Если взаимнопростые p и q делят x, то p·q также делит x.

Скомбинировав вышесказанное и применив принцип включений-исключений получаем, что

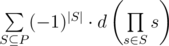
считая, что произведение пустого множества равно 1. Итак, мы получили сумму из 2|P| слагаемых, но большая часть из них не вносит вклада в ответ, т.к. соответствующее произведение превышает 10⁵. Можно непосредственно нагенерить нужные произведения, а можно просто пройтись по [1;10⁵], отбрасывая числа, не являющиеся произведениями простых (например, это можно проверить за логарифм, посчитав наименьший простой делитель в решете). Я воспользовался 2-м вариантом, и у меня получилось такое решение: 33406195

Сдав задачу, я заглянул в разбор, а там

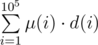
Я посмотрел в код. Посмотрел в разбор. И снова в код. Функция sign(x), возвращающая знак слагаемого, как раз и есть функция Мёбиуса:

int sign(int x) {
	//lp[x] - наименьший простой делитель, а quot[x] - это x / lp[x]
	int prev = -1;
	int sgn = 1;
	for(; x > 1; x = quot[x]) { 
		if (lp[x] == prev) return 0;
		prev = lp[x];
		sgn = -sgn;
	}  
	return sgn;
}

Почему во включениях-исключениях всплыла функция Мёбиуса? Совпадение? Не думаю.

Я осознал, что мало знаю о включениях и исключениях и пошёл гуглить. Оказалось, что помимо привычной μ(x) для целых чисел, существует обобщенная функция Мёбиуса μ(x, y) для любого множества объектов с заданным отношением порядка. Для μ(x, y) также справедлив аналог формулы обращения Мёбиуса. А формула включений-исключений является частным случаем обобщённой формулы обращения Мёбиуса. Подробности можно почитать хотя бы на википедии, копипастить я не буду. Мне захотелось вывести решение рассматренной задачки, используя новые знания. И вот что получилось.

Рассмотрим множество [1;10⁵] с отношением делимости |, как отношением нестрогого частичного порядка (нетрудно убедиться, что необходимым свойствам это отношение удовлетворяет). Пусть g(x) — количество подпоследовательностей, НОД которых равен x, тогда введенную ранее функцию d(x) можно выразить так:

Теперь применим обобщённую формулу обращения, получив выражение для