Somehow I managed to solve 901B - GCD of Polynomials however I don't know why my solution works. My idea was to pick two random polynomials of degrees n and n-1 check how many steps it takes to find the gcd and return the polynomials if the answer is n. However doing the gcd over 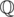 is hard because of fractions. So I decided to pick a prime and do gcds over the finite field Fp. The strange thing is with a bigish prime like 1009 the algorithm took more steps over this field than over
is hard because of fractions. So I decided to pick a prime and do gcds over the finite field Fp. The strange thing is with a bigish prime like 1009 the algorithm took more steps over this field than over 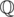 . Then I tried using the prime 43 just to see what would happen and it worked.
. Then I tried using the prime 43 just to see what would happen and it worked.
code






