Somehow I managed to solve 901B - GCD of Polynomials however I don't know why my solution works. My idea was to pick two random polynomials of degrees n and n-1 check how many steps it takes to find the gcd and return the polynomials if the answer is n. However doing the gcd over 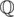 is a pain because of fractions. If you try to avoid them by multiplication by denominators things overflow pretty quickly.
is a pain because of fractions. If you try to avoid them by multiplication by denominators things overflow pretty quickly.
So I decided to pick a prime and do gcds over the finite field Fp. The strange thing is with a medium sized prime like 1009 the algorithm took more steps over this field than over 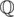 . Then I tried using the prime 43 just to see what would happen, since it worked on the case where 1009 gave an incorrect answer. Surprisingly using 43 worked for all the cases. Anyone know of a special relationship between the number of steps the Euclidean algorithm for polynomials takes over
. Then I tried using the prime 43 just to see what would happen, since it worked on the case where 1009 gave an incorrect answer. Surprisingly using 43 worked for all the cases. Anyone know of a special relationship between the number of steps the Euclidean algorithm for polynomials takes over 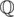 and Fp for a given prime p?
and Fp for a given prime p?






