Hi. I am trying to solve this problem.
For convenience, I have summarized the problem statement below.
Problem Statement
Given an array of length ≤ 2e6 containing integers in the range [0, 1e6], find the longest subarray that contains a majority element (i.e. an element that occurs > ⌊ N / 2⌋ times in a list of length N).
Time limit: 1.5s
Example
If the given array is [1, 2, 1, 2, 3, 2],
The answer is 5 because the subarray [2, 1, 2, 3, 2] from position 1 to 5 (0-indexed) has the number 2 which appears 3 > ⌊ 5 / 2⌋ times. Note that we cannot take the entire array because 3 = ⌊ 6 / 2⌋ .
My attempt
The first thing that comes to mind is an obvious brute force (but correct) solution which fixes the start and end indexes of a subarray and loop through it to check if it contains a majority element. Then we take the length of the longest subarray that contains a majority element. This works in 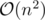 after a small optimization. Clearly, this will not pass the time limit.
after a small optimization. Clearly, this will not pass the time limit.
I also tried asking the same question on stack overflow, but did not receive a satisfactory answer (after several wrong suggestions and much discussion, I tried implementing the answer by Pham Trung that was given in the link, but it seems to fail on this case: [3, 3, 5, 2, 4, 1, 5]).
Could someone please advise me on a better approach to solve this problem?






