Hi. I am trying to solve this problem.

For convenience, I have summarised the problem statement below:

Problem Statement

We are tasked to arrange X Apples, Y Cherries and Z mangoes on a line, Compute the number of valid arrangements (modulo 1e9 + 7). All X + Y + Z fruits must be used in a single arrangement.

A valid arrangement is defined as an arrangement in which no two fruits of a similar kind are adjacent (no wraparound).

Constraints: 1 ≤ X, Y, Z ≤ 2e5 Time limit: 2s

Example

Example of a valid arrangement for X = 2, Y = 2, Z = 2 is:

Apple Orange Cherry Apple Orange Cherry

Example of a invalid arrangement for X = 2, Y = 2, Z = 2 is:

Apple Apple Orange Cherry Orange Cherry

My analysis

If the constraints were smaller, an obvious 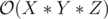dynamic programming solution would suffice. However, the large constraints here seem to point towards a combinatorics solution (which I cannot figure out).

Could someone please advise me on how to solve this problem?