Consider the following problem:
We are given N sets {S1, ..., SN} of integers, with 1 ≤ |Si| ≤ 16 (i.e. no set is empty or has more than 16 elements) and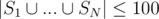 
. We want to partition the given sets into the minimum number of partitions such that the number of elements in the union of all sets in any partition doesn't exceed given constant K ≤ 16.
Is there a way to sort the sets such that the partitions of the optimal solution are contiguous? (in which case a DP solution to the original problem follows). How to prove such properties for other partition cost functions in general?
Thanks!
P.S.: I found this: https://books.google.co.uk/books?id=PD3ICgAAQBAJ&pg=PA293&lpg=PA293&dq=Partition+Problems+over+Single-Parameter+Spaces:+Combinatorial+Approach&source=bl&ots=FdNvNpE_96&sig=MQOnuezKZfMUbyACjqZq5adR_rM&hl=en&sa=X&ved=0ahUKEwjrj67K7qTZAhVkJMAKHXW0APIQ6AEILjAA#v=onepage&q&f=false but unfortunately is not available in full.
