Codeforces 977D Editorial

977D — Divide by three, multiply by two

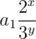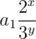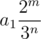
We can see that all numbers in given sequence are distinct. since all numbers in sequence are of the form $\text{[math]}$ . Hence if a_i = a_j then 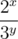$\text{[math]}$ = $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ = $\text{[math]}$ $\text{[math]}$ 2^x - m = 3^y - n which is not possible because any power of 2 will be an even number and any power of 3 will be an odd number.
if there exists 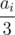$\text{[math]}$ in sequence then 2 * a_i can not be in sequence and vice versa. We can prove it using contradiction. Suppose there is a number a_i such that both 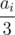$\text{[math]}$ and 2 * a_i exists in sequence. by little bit of tricks this 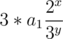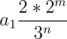$\text{[math]}$ $\text{[math]}$ = $\text{[math]}$ , this again is not possible by same argument as above, we just have to change the order of exponents.
Hence for each a_i in sequence we see if 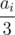$\text{[math]}$ or 2 * a_i is present(remember that only one of them can be present). Now if there is any a_i such that both 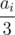$\text{[math]}$ and 2 * a_i is not in sequence then this should be a_n. if there is any such a_i that for all 0 ≤ j ≤ n: $\text{[math]}$ ≠ a_i AND 2 * a_i ≠ a_i, then this is a₁.
Once you have got a₁, you keep on producing sequence just by doing binary search for 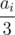$\text{[math]}$ and 2 * a_i (remember only one of them is present so once you find it you print it).

Rev.	By	When	Δ	Comment
en11	aMitkvikram	2018-06-21 20:00:24	13
en10	aMitkvikram	2018-06-21 19:59:23	14
en9	aMitkvikram	2018-06-21 19:58:14	46	Tiny change: '^m}{3^n}$ which is n' -> '^m}{3^n}$ $\implies$ $2^{x - m} = 3^{y - n}$which is n'
en8	aMitkvikram	2018-05-07 16:44:43	2	(published)
en7	aMitkvikram	2018-05-07 16:43:12	2	Tiny change: 'eq$ $j\leq$ $\dfrac{' -> 'eq$ $j\leqn:$ $\dfrac{'
en6	aMitkvikram	2018-05-07 16:42:31	5
en5	aMitkvikram	2018-05-07 16:41:49	3	Tiny change: 'l $0\leq$ j $ $\leq$ $\' -> 'l $0\leq$ $j $\leq$ $\'
en4	aMitkvikram	2018-05-07 16:41:03	17
en3	aMitkvikram	2018-05-07 16:39:32	5
en2	aMitkvikram	2018-05-07 16:37:18	1244	Tiny change: 'n4. Once yuou have go' -> 'n4. Once you have go'
en1	aMitkvikram	2018-05-07 16:17:24	339	Initial revision (saved to drafts)